【ストリング図で学ぶ圏論 番外編2】線形代数の圏論的な性質（？）を圏論なしで説明する

はじめに

圏論の基礎的な概念を学ぶと，その具体例として，「集合と写像」や「ベクトル空間と線形写像」に関する数学的な構造などに関する知見が得られます。この記事では，このような知見のうち，線形代数に関して「知っておいて損はない」と思うものをいくつか紹介します。圏論の知識がなくても理解できることをめざしました（補足では，圏論の話題に触れることがあります）。この記事で紹介する概念は，線形代数の式をストリング図とよばれる図式で表す際にも役立ちます。

以降では，集合論と線形代数の共通点と相違点に着目しながら説明します。集合と写像や線形代数に関する基礎知識はあるものとします。この記事では，次の4個の話題について説明します。

1. ベクトル空間の各要素は線形写像とみなせる
2. 有限次元の線形代数は自己双対的
3. 自由ベクトル空間と忘却写像
4. ベクトル空間の直積とテンソル積

本連載の目次

#1： 圏の定義と具体例
#2： 関手と自然変換
#3： 垂直合成と水平合成
#4： モノイダル圏
#5： モナドとは自己関手の圏におけるモノイド対象のこと
#6： モナドの例
#7： 随伴
#8： 関手を表す線の順序の交換
#9： 普遍射と随伴・極限・カン拡張
#10： ホム関手のストリング図（前編）
#11： ホム関手のストリング図（後編）
#12： 米田の補題
番外編1： 視覚的に理解するクライスリトリプルとモナドの同値性
番外編2： 線形代数の圏論的な性質（？）を圏論なしで説明する（この記事）

準備

集合論

集合の集まりを$\mathbf{Set}$と書きます。また，集合$X$から集合$Y$への写像全体からなる集合を$\mathbf{Set}(X,Y)$と書きます。1点集合（1個の要素からなる集合）を代表して，$\{\ast \}$と書きます（$\ast$がこの集合の唯一の要素です）。有限個の要素のみをもつ集合$X$を有限集合とよび，その要素数を$|X|$と書きます。

線形代数

実数全体からなる集合を$\mathbb{R}$とおき，実ベクトル空間の集まりを${\mathbf{Vec}}_{\mathbb{R}}$と書きます。また，実ベクトル空間$\mathbf{V}$から実ベクトル空間$\mathbf{W}$への線形写像全体からなる集合を${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbf{W})$と書きます。$\mathbb{R}$は1次元実ベクトル空間です。なお，話を簡単にするため，この記事では実ベクトル空間に限定して話をしますが，一般の体上のベクトル空間を考えてもこの記事で説明することはほぼ成り立ちます。

各ベクトル空間$\mathbf{V},\mathbf{W}$について，集合${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbf{W})$はベクトル空間とみなせます。以降では，しばしばこの事実を用います。

要素と写像の同一視

集合論の場合

任意の集合$X$の要素は，$\{\ast \}$から$X$への写像と同一視できることを述べます。この同一視により，集合の要素を「写像の特別な場合」とみなすことができます。

集合の要素と$\{\ast \}$からの写像との同一視

各集合$X$について，この同型が成り立つことは「$X$の各要素は$\{\ast \}$から$X$への写像とみなせる（かつこの対応は一対一である）」ことを意味しています。この証明から，$\mathbf{Set}(\{\ast \},X)$のすべての要素は$\tilde{x}$$(x\in X)$の形で表せます。以降では，$x$と$\tilde{x}$を同一視します。

$x\in X$の図式表現

$x\in X$は次の二通りの図式で表せます。

$x\in X$

左側の図式における長方形のブロック$x$は，写像$x:\{\ast \}\to X$のことだとみなせます。なお，ここでは先述の$\tilde{x}$を$x$と書いています（これらを同一視しているのでした）。ブロックの下側および上側から伸びた線が，それぞれ$x$の始域$\{\ast \}$および終域$X$を表しています。このように，ブロックが写像を表し，線が集合を表します。また，1点集合$\{\ast \}$を表す線は省略できるものとします。この省略により，左側の図式は右側の図式のように表せます。

要素$x\in X$と写像$f:X\to Y$に対し，$f(x)$は次の図式で表せます。

$f(x)$

ブロック$f$とブロック$x$が線$X$によりつながっていますが，これは写像としての合成$f\circ x$（つまり$\{\ast \}\stackrel{x}{\mapsto }X\stackrel{f}{\mapsto }Y$を表すと考えてください。このように，ブロック同士の直列接続は写像としての合成を表します。2個のブロック$f$と$x$をグループ化して1個のブロックと解釈すれば，写像$f\circ x:\{\ast \}\to Y$を表していることが視覚的に理解できるかと思います。先ほどの同一視により，この写像$f\circ x$は要素$f(x)$と同一視されます。

集合論では，上のように写像をブロックで表すような図式を用いるとしばしば便利です。

線形代数の場合

集合論の場合と同様に，任意のベクトル空間$\mathbf{V}$の要素は，$\mathbb{R}$から$\mathbf{V}$への線形写像と同一視できます。この同一視により，ベクトル空間の要素を「線形写像の特別な場合」とみなすことができます。

ベクトルと$\mathbb{R}$からの線形写像との同一視

線形代数でも，命題1に相当する次の命題が成り立ちます。

この意味で，集合論における$\{\ast \}$と線形代数における$\mathbb{R}$が対応しています。

この同型が成り立つことは，「各ベクトル空間$\mathbf{V}$の各要素は$\mathbb{R}$から$\mathbf{V}$への線形写像とみなせる（かつこの対応は一対一である）」ことを意味しています。この命題から，${\mathbf{Vec}}_{\mathbb{R}}(\mathbb{R},\mathbf{V})$のすべての要素は$\text{–}\cdot v$$(v\in \mathbf{V})$の形で表せます。以降では，$v$と$\text{–}\cdot v$を同一視します。

$v\in \mathbf{V}$の図式表現

集合論の場合と同様に，ブロックが線形写像を表し，線がベクトル空間を表すような図式が考えられます。$v\in \mathbf{V}$は線形写像$\text{–}\cdot v:\mathbb{R}\to \mathbf{V}$と同一視されますので，二通りの図式で表せます。

$v\in \mathbf{V}$

この図式では，右側の図式のように線$\mathbb{R}$を省略できるものとします。

ブロック同士の直列接続は写像としての合成を表します。たとえば，要素$v\in \mathbf{V}$と線形写像$f:\mathbf{V}\to \mathbf{W}$に対し，$f(x)$は次の図式で表せます。

$f(v)$

線形代数では，上のように線形写像をブロックで表すような図式がしばしば活躍します。

参考：$\{\ast \}$への写像と$\mathbb{R}$への線形写像との比較

上の議論では，集合論における1点集合$\{\ast \}$と線形代数における実数全体$\mathbb{R}$が対応していました。しかし，$\{\ast \}$からの写像（または$\mathbb{R}$からの線形写像）を考える代わりに，$\{\ast \}$への写像（または$\mathbb{R}$への写像）について考えると，話が変わってきます。

集合論において$\{\ast \}$への写像を考えると，$\mathbf{Set}(\{\ast \},X)\cong X$に似た式として$\mathbf{Set}(X,\{\ast \})\cong \{\ast \}$が成り立つことがわかります。実際，各集合$X$について，$X$から$\{\ast \}$への写像は各$x\in X$を$\ast \in \{\ast \}$に写すものしか存在せず，したがって集合$\mathbf{Set}(X,\{\ast \})$は1点集合です。つまり，$\mathbf{Set}(X,\{\ast \})$は$\{\ast \}$と同型です。

一方，線形代数ではこれに相当する式である${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbb{R})\cong \mathbb{R}$は成り立ちません（$\dim \mathbf{V}=1$の場合は例外）。これらを次の表にまとめておきます。

なお，$\mathbf{V}$が有限次元ならば${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbb{R})\cong \mathbf{V}$が成り立ち，したがって${\mathbf{Vec}}_{\mathbb{R}}(\mathbb{R},\mathbf{V})\cong \mathbf{V}\cong {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbb{R})$のような対称性（自己双対性とよびます）が成り立ちます。自己双対性については，これから説明します。

有限次元に限定した線形代数は自己双対的

有限次元ベクトル空間$\mathbf{V},\mathbf{W}$を任意に選びます。このとき，ベクトル空間として
$${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbf{W})\cong {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{W},\mathbf{V})$$
が成り立ちます。実際，$N:=\dim \mathbf{V}$および$M:=\dim \mathbf{W}$とおくと，${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbf{W})$の各要素は$M$行$N$列の行列と一対一に対応し，${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{W},\mathbf{V})$の各要素は$N$行$M$列の行列と一対一に対応します。また，行列の転置により$M$行$N$列の行列と$N$行$M$列の行列は一対一に対応するため，上の同型が成り立ちます（厳密な証明は割愛しますが，この直観的な説明に基づけば容易に示せます）。より端的に述べると，${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbf{W})$ と${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{W},\mathbf{V})$はどちらも$MN$次元ベクトル空間ですので，同型です。

${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbf{W})$から${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{W},\mathbf{V})$への可逆な線形写像（たとえば，上の例における転置）を一つ選んで$†$とおきます。この写像は次の図式で表せます。

$f$とその双対$f^{†}$

ただし，各$f\in {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbf{W})$の写り先$†(f)$を$f^{†}$と書き，$f$の双対とよぶことにします。直観的には，この写像は「図式を上下反転させる」ようなはたらきをしているといえます。なお，「上下反転」であることを視覚的に示すために，ブロックの形状を長方形ではなく台形で表しました。

とくに，ベクトル空間${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbb{R})$を$\mathbf{V}$の双対ベクトル空間とよび，${\mathbf{V}}^{\ast }$と書きます。上の同型において$\mathbf{W}=\mathbb{R}$の場合を考えれば，$\mathbf{V}$と${\mathbf{V}}^{\ast }$が同型であることが，次式からわかります。
$$\mathbf{V}={\mathbf{Vec}}_{\mathbb{R}}(\mathbb{R},\mathbf{V})\cong {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},\mathbb{R})={\mathbf{V}}^{\ast }$$

先ほどの図式と同様に，各$v\in \mathbf{V}$をその双対$v^{†}\in {\mathbf{V}}^{\ast }$に写す写像$†$は，次の図式で表されます。

$v$とその双対$v^{†}$

ブロック$v$の下側から伸びた線$\mathbb{R}$と，ブロック$v^{†}$の上側から伸びた線$\mathbb{R}$を，ともに省略しています。直観的には，$v^{†}$は$v$の「上下反転」といえます。$f(v)\in \mathbf{W}$は写像$†$により$(f(v){)}^{†}\in {\mathbf{W}}^{\ast }$に写ります。

$f(v)$とその双対$(f(v){)}^{†}$

$f(v)$が$f$と$v$の写像としての合成$f\circ v$とみなせるのに対し，$(f(v){)}^{†}$は$v^{†}$と$f^{†}$の写像としての合成$v^{†}\circ f^{†}$とみなせます。$f^{†}\circ v^{†}$ではなく$v^{†}\circ f^{†}$である理由は，図式が「上下反転」の関係にあることから直観的に理解できるかと思います。

このような意味で，有限次元ベクトル空間とその間の線形写像は，「双対をとっても数学的な構造は変わらない」といえます。このような性質は，自己双対とよばれます。

より直観的な説明として，$N$行$M$列の行列$F$を考えます。この行列は，次の線形写像
$$F\cdot \text{–}:{\mathbb{R}}^M\ni v\mapsto F\cdot v\in {\mathbb{R}}^N$$

と一対一に対応しており，通常は行列$F$と線形写像$F\cdot \text{–}$は同一視されるかと思います。一方で，行列$F$は次の線形写像
$$\text{–}\cdot F:({\mathbb{R}}^N{)}^{\ast }\ni w\mapsto w\cdot F\in ({\mathbb{R}}^M{)}^{\ast }$$
とも一対一に対応しており，これらを同一視しても問題ありません（なお，$({\mathbb{R}}^N{)}^{\ast }={\mathbf{Vec}}_{\mathbb{R}}({\mathbb{R}}^N,\mathbb{R})$の各要素$w$は，$N$次元行ベクトルとみなせます）。このように，行列$F$を「列ベクトルを列ベクトルに写す写像」$F\cdot \text{–}$と捉えても，「行ベクトルを行ベクトルに写す写像」$\text{–}\cdot F$と捉えても，本質的には何も問題ないといえます。大ざっぱには，自己双対とはこのような関係のことだといえます。なお，写像$\text{–}\cdot F$は，転置をとると次の線形写像
$$F^{\mathrm{T}}\cdot \text{–}:{\mathbb{R}}^N\ni w^{\prime }\mapsto F^{\mathrm{T}}\cdot w^{\prime }\in {\mathbb{R}}^M$$
になります（${}^{\mathrm{T}}$は転置）。つまり，行列$F$は写像$F^{\mathrm{T}}\cdot \text{–}$ともみなせます。

自由ベクトル空間と忘却写像の関係

集合の集まり$\mathbf{Set}$と実ベクトル空間の集まり${\mathbf{Vec}}_{\mathbb{R}}$の間にある特徴的な性質について述べます。

各集合$X$に対して，「$X$を基底とするような実ベクトル空間」を$X$の自由ベクトル空間とよび，$\mathrm{Free}(X)$と表すことにします。有限次元ベクトル空間の次元はその基底の要素数に等しいため，各有限集合$X$についてベクトル空間$\mathrm{Free}(X)$の次元は$|X|$です。

写像$\mathbf{Set}\ni X\mapsto \mathrm{Free}(X)\in {\mathbf{Vec}}_{\mathbb{R}}$を$\mathrm{Free}$と書き，自由写像とよぶことにします。

各ベクトル空間$\mathbf{V}$について，$\mathbf{V}$に備わっている和と実数倍という演算を忘れて，$\mathbf{V}$を単なる集合とみなしたものを$U\mathbf{V}$と書くことにします。このとき，次の命題が成り立つことがわかります。

この同型は，$\mathrm{Free}(X)$から$\mathbf{W}$への線形写像と，$X$から$U\mathbf{W}$への写像が一対一に対応することを意味しています。

写像${\mathbf{Vec}}_{\mathbb{R}}\ni \mathbf{W}\mapsto U\mathbf{W}\in \mathbf{Set}$を$U$と書き，（和と実数倍を忘れるという意味で）忘却写像とよぶことにします。自由写像$\mathrm{Free}$と忘却写像$U$は上の意味で密接に関係しており，このような関係は随伴とよばれます。

上の証明より，各$f\in {\mathbf{Vec}}_{\mathbb{R}}(\mathrm{Free}(X),\mathbf{W})$を写像$\bar{f}:X\ni x\mapsto f(x)\in U\mathbf{W}$に写すような写像$\mathrm{\Psi }:{\mathbf{Vec}}_{\mathbb{R}}(\mathrm{Free}(X),\mathbf{W})\to \mathbf{Set}(X,U\mathbf{W})$は可逆です。この写像$\mathrm{\Psi }$は，次の図式のように表せます。

同型${\mathbf{Vec}}_{\mathbb{R}}(\mathrm{Free}(X),\mathbf{W})\cong \mathbf{Set}(X,U\mathbf{W})$を与える写像

ただし，（ブロック$f$の下側の）線$X$の左右にある2本の青線は自由写像$\mathrm{Free}$を表しており（この2本の線に挟まれた$X$が$\mathrm{Free}$への入力です），ブロック$f$は${\mathbf{Vec}}_{\mathbb{R}}(\mathrm{Free}(X),\mathbf{W})$の要素です。また，（ブロック$\bar{f}$の上側の）線$\mathbf{W}$の左右にある2本の青線は忘却写像$U$を表しており，ブロック$\bar{f}$は$\mathbf{Set}(X,U\mathbf{W})$の要素です。直観的には，$\mathrm{Free}$と$U$が随伴の関係にあることは，「ブロック$f$の下側にある2本の青線のペア$\mathrm{Free}$を，（可逆写像$\mathrm{\Psi }$により）ブロックの上側にある2本の青線のペア$U$に置き換えられる」ことといえそうです（このとき，ブロック$f$はブロック$\bar{f}$に置き換えられます）。可逆写像$\mathrm{\Psi }$の逆写像は，各$\bar{f}$を$f$に写します。

直積とテンソル積

線形代数における直積とテンソル積は，どちらもある意味では「2個の集合$X,Y$の直積$X\times Y$に相当する概念」といえることを説明します。

線形代数における直積

集合論の場合

集合$X$と集合$Y$の直積とは，集合$\{⟨x,y⟩\mid x\in X,y\in Y\}$（つまり$X$の各要素$x$と$Y$の各要素$y$の組$⟨x,y⟩$をすべて集めた集合）のことです。

次の命題は，集合の直積$X\times Y$を特徴付けます。

写像
$$\mathrm{copy}:Z\ni z\mapsto ⟨z,z⟩\in Z\times Z$$
を考えて，次の図式で表すことにします。

写像$\mathrm{copy}$

ここで，右辺の黒丸は写像$\mathrm{copy}$を表しています。「特別な写像」であるという雰囲気を出すために，ブロックではなく黒丸として表しました。線$X$と線$Y$を横に並べることで，$X\times Y$を表すことにします。つまり，集合の直積を「2本の線を横に並べる」ことで表すことにします。この図式（左辺および右辺）から，$\mathrm{copy}$は$Z$から$Z\times Z$への写像であることが読み取れます。

$f$が写像$Z\ni z\mapsto ⟨f_1(z),f_2(z)⟩\in X\times Y$の形で表せることは，$f=⟨f_1,f_2⟩\circ \mathrm{copy}$の形で表せることを意味しています。ただし，写像の組$⟨f_1,f_2⟩$を写像
$$⟨f_1,f_2⟩:Z\times Z\ni ⟨z,z^{\prime }⟩\mapsto ⟨f_1(z),f_2(z^{\prime })⟩\in X\times Y$$

とみなします。$f=⟨f_1,f_2⟩\circ \mathrm{copy}$は，次の図式で表せます。

$f=⟨f_1,f_2⟩\circ \mathrm{copy}$

ここで，2個のブロック$f_1$と$f_2$を横に並べることで，写像$⟨f_1,f_2⟩$を表しています。
式$\text{(2)}$の同型は，$f\in \mathbf{Set}(Z,X\times Y)$と$⟨f_1,f_2⟩\in \mathbf{Set}(Z,X)\times \mathbf{Set}(Z,Y)$が一対一に対応することを表しています。

線形代数の場合

ベクトル空間の直積$\mathbf{V}\times \mathbf{W}$を定義しておきましょう。$\mathbf{V}$と$\mathbf{W}$の直積とは，「$\mathbf{V}$と$\mathbf{W}$の集合としての直積$\mathbf{V}\times \mathbf{W}$」に対して和と実数倍を適切に定めることでできるベクトル空間のことと定義できます。具体的には，和は，集合$\mathbf{V}\times \mathbf{W}$の2個の各要素$⟨v,w⟩,⟨v^{\prime },w^{\prime }⟩$に対して$⟨v,w⟩+⟨v^{\prime },w^{\prime }⟩:=⟨v+v^{\prime },w+w^{\prime }⟩$と定めます。また，実数倍は，集合$\mathbf{V}\times \mathbf{W}$の要素$⟨v,w⟩$と実数$r$に対して$r⟨v,w⟩:=⟨rv,rw⟩$と定めます。このとき，$\mathbf{V}\times \mathbf{W}$がベクトル空間になることが容易に確認できます。

集合論の場合と同様に，線形代数でも次の命題が成り立ちます。

集合論の場合と同様に，線形写像$\mathrm{copy}:\mathbf{X}\ni x\mapsto ⟨x,x⟩\in \mathbf{X}\times \mathbf{X}$を用いると，$f=⟨f_1,f_2⟩\circ \mathrm{copy}$と表せます。図式では，次のように表せます。

$f=⟨f_1,f_2⟩\circ \mathrm{copy}$

この図式では，ベクトル空間の直積を「2本の線を横に並べる」ことで表しています。ただし，後で述べるテンソル積の場合と区別するために，背景色を（黄色ではなく）緑色としました。

なお，${\mathbf{Vec}}_{\mathbb{R}}$における直積は，直和とよばれるものと同一視できます（直積$\mathbf{V}\times \mathbf{W}$と直和$\mathbf{V}\oplus \mathbf{W}$はベクトル空間として同型です）。

備考：集合の直積とベクトル空間の直積の比較？

1次元以上の実ベクトル空間は無限集合です。しかし，ある観点では，有限集合に対応する線形代数の概念は，（基底が有限集合という意味で）有限次元ベクトル空間かもしれません。このような対応を考えたとき，集合$X$の要素数$|X|$に相当する線形代数の概念は，ベクトル空間$\mathbf{V}$の次元$\dim \mathbf{V}$といえそうです。

集合の要素数とベクトル空間の次元の間には，次の表のような関係があることがわかります。ただし，要素数$N$の集合$X$と要素数$M$の集合$Y$を考え，また$N$次元ベクトル空間$\mathbf{V}$と$M$次元ベクトル空間$\mathbf{W}$を考えています。

このように，集合の要素数の積$MN$およびべき乗$M^N$が，ベクトル空間の次元の和$M+N$および積$MN$に対応しています。

線形代数におけるテンソル積

集合論の場合（直積）

式$\text{(2)}$は「$X\times Y$への写像」に関する性質といえます。集合の直積は，これに対応する「$X\times Y$からの写像」に関する次の命題も満たします。

直観的には，$f$は「$x$と$y$を同時に入力すると，$f(x,y)$を出力する」という写像を表しており，$\tilde{f}$は「最初に$x$を入力して次に$y$を入力すると，$f(x,y)$を出力する」という写像を表しているといえます。

集合$\mathbf{Set}(Y,Z)$を次の図式で表すことにします。

集合$\mathbf{Set}(Y,Z)$

このとき，写像$g\in \mathbf{Set}(Y,Z)$は次の右辺のような図式でも表せます。

$g\in \mathbf{Set}(Y,Z)$を表す二通りの図式

直観的には，下向きの矢印$Y$はブロック$g$への入力だと捉えられます。矢印が付いていない線は上向きの矢印のことだと考えて，この図式は

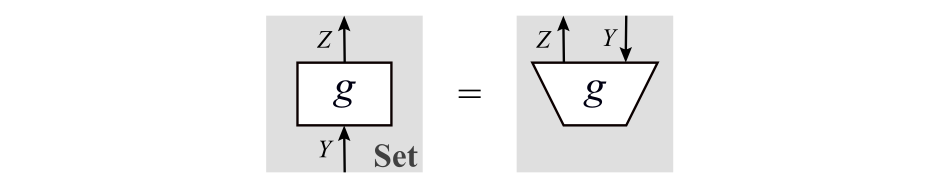上向きの矢印を付けた図式

のことだと考えると，左辺と右辺はともに$Y$が入力で$Z$が出力であることがイメージしやすいと思います。左辺のようにブロック$g$の下側に描かれた線$Y$を，右辺のように下向きの矢印で表してブロック$g$の上側に描けると考えてください。また，左辺と右辺ではブロック$g$の形状が異なりますが，これは単なる描画の都合によるもので本質的な違いはありません。

$f\in \mathbf{Set}(X\times Y,Z)$と$\tilde{f}\in \mathbf{Set}(X,\mathbf{Set}(Y,Z))$は，それぞれ次の図式で表されます。

$f$と$\bar{f}$

これらはともに2入力の写像である（具体的には，線$X$と線$Y$が入力で$Z$が出力である）ことから，直観的には「同じようなもの」であることがわかるでしょう。

線形代数の場合

式$\text{(4)}$に相当する線形代数の式を考えたいのですが，残念ながらベクトル空間$\mathbf{V},\mathbf{W},\mathbf{X}$に対して一般に
$${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V}\times \mathbf{W},\mathbf{X})\ncong {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},{\mathbf{Vec}}_{\mathbb{R}}(\mathbf{W},\mathbf{X}))$$
です。しかし，直積$\mathbf{V}\times \mathbf{W}$をこれから定義するテンソル積$\mathbf{V}\otimes \mathbf{W}$に置き換えれば，この同型が成り立つことがわかります。

2個のベクトル空間$\mathbf{V}$と$\mathbf{W}$のテンソル積$\mathbf{V}\otimes \mathbf{W}$は，$\mathbf{V}$の基底$B_{\mathbf{V}}:=\{{\varphi }_i{\}}_i$と$\mathbf{W}$の基底$B_{\mathbf{W}}:=\{{\psi }_j{\}}_j$に対して，これらの基底の集合としての直積$B_{\mathbf{V}}\times B_{\mathbf{W}}=\{⟨{\varphi }_i,{\psi }_j⟩{\}}_{i,j}$を基底とするようなベクトル空間，つまり$\mathbf{V}\otimes \mathbf{W}:=\mathrm{Free}(B_{\mathbf{V}}\times B_{\mathbf{W}})$として定義できます（和と実数倍は素直な方法で定められます）。

次の命題が成り立ちます。

上では，テンソル積$\mathbf{V}\otimes \mathbf{W}$の定義（の一つ）を明示的に示して式$\text{(5)}$を導きました。逆に，式$\text{(5)}$を満たすような$\mathbf{V}\otimes \mathbf{W}$をテンソル積と定義することもできます。とくに，証明の途中で現れた$\mathbf{Set}(B_{\mathbf{V}}\times B_{\mathbf{W}},U\mathbf{X})$は「$\mathbf{V}\times \mathbf{W}$から$\mathbf{X}$への双線形写像の集合」とみなせますので，「$\mathbf{V}\times \mathbf{W}$から$\mathbf{X}$への双線形写像」と「$\mathbf{V}\otimes \mathbf{W}$から$\mathbf{X}$への線形写像」が一対一に対応するようにテンソル積$\mathbf{V}\otimes \mathbf{W}$を定めることもできます。このような定義は，たとえば拙著Nak-2022のA.6節をご参照ください。

ベクトル空間のテンソル積では，集合論の場合と同様の図式が利用できます。集合論では集合$\mathbf{Set}(Y,Z)$を「線$Z$と下向きの矢印$Y$を横に並べる」ことで表しました。これと同様に，線形代数ではベクトル空間${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{W},\mathbf{X})$を「線$\mathbf{X}$と下向きの矢印$\mathbf{W}$を横に並べる」ことで表すことにします。

ベクトル空間${\mathbf{Vec}}_{\mathbb{R}}(\mathbf{W},\mathbf{X})$

このとき，$f\in {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V}\otimes \mathbf{W},\mathbf{X})$と$\tilde{f}\in {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},{\mathbf{Vec}}_{\mathbb{R}}(\mathbf{W},\mathbf{X}))$は，それぞれ次の図式で表されます。

$f$と$\bar{f}$

ただし，線$\mathbf{V}$と線$\mathbf{W}$を横に並べることで$\mathbf{V}\otimes \mathbf{W}$を表しています。$f$と$\tilde{f}$はともに2入力の写像とみなせる（具体的には，線$\mathbf{V}$と線$\mathbf{W}$が入力で$\mathbf{X}$が出力である）ことから，直観的には「同じようなもの」であることがわかるでしょう。

式$\text{(2)}$～$\text{(5)}$をまとめて再掲しておきます。

$$\begin{array}{rlr}\mathbf{Set}(Z,X\times Y)& \cong \mathbf{Set}(Z,X)\times \mathbf{Set}(Z,Y)& \text{(2)}\\ {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{X},\mathbf{V}\times \mathbf{W})& \cong {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{X},\mathbf{V})\times {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{X},\mathbf{W})& \text{(3)}\\ \mathbf{Set}(X\times Y,Z)& \cong \mathbf{Set}(X,\mathbf{Set}(Y,Z))& \text{(4)}\\ {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V}\otimes \mathbf{W},\mathbf{X})& \cong {\mathbf{Vec}}_{\mathbb{R}}(\mathbf{V},{\mathbf{Vec}}_{\mathbb{R}}(\mathbf{W},\mathbf{X}))& \text{(5)}\end{array}$$

すでに述べたように，集合論における直積は式$\text{(2)}$,$\text{(4)}$をともに満たします。一方，線形代数においては，これらの式に対応する式は$\text{(3)}$,$\text{(5)}$となります。この観点では，集合論における直積$X\times Y$に対応する線形代数の概念は，直積$\mathbf{V}\times \mathbf{W}$とテンソル積$\mathbf{V}\otimes \mathbf{W}$の二つといえるでしょう。

まとめ

この記事では，圏論の基礎的な概念と密接な関係にあるいくつかの概念を説明しました。これらの概念は，線形代数を図式で表す際にも活用できます。また，これらの概念を知っていれば，圏論の基礎を学ぶ際にも役立つと思います。