文献あり

【ストリング図で学ぶ圏論 #7】随伴

121

はじめに

随伴は，圏論における基礎的な概念の一つであり，数学のいたるところで現れます。また，第5回と第6回の記事で述べたモナドは，随伴と密接な関係にあります。この記事では，随伴の2通りの同値な定義を紹介し，またモナドと随伴の関係などについて述べます。

補足：

随伴の定義として普遍射を用いるものについてはこの記事では述べません。第9回の記事で触れることにします。

本連載の目次

#1：圏の定義と具体例
#2：関手と自然変換
#3：垂直合成と水平合成
#4：モノイダル圏
#5：モナドとは自己関手の圏におけるモノイド対象のこと
#6：モナドの例
#7：随伴（この記事）

随伴の定義

定義1：2個の自然変換を用いた定義

随伴は次のように定義されます。慣れないうちはこの定義のココロを理解することは難しいと思いますが，気にせずに読み進めてください。

随伴

関手$F \colon \cC \to \cD$と関手$G \colon \cD \to \cC$を考える。自然変換$\eta \colon 1_\cC \nto G \b F$と自然変換$\varepsilon \colon F \b G \nto 1_\cD$が存在して
$$ (1_G \b \varepsilon) \c (\eta \b 1_G) = 1_G, \quad (\varepsilon \b 1_F) \c (1_F \b \eta) = 1_F $$ $$\tag{1}\label{eq:1}$$
を満たすとき，組$\braket{F,G,\eta,\varepsilon}$を随伴とよぶ。また，$\eta$を単位とよび，$\varepsilon$を余単位とよぶ。

なお，恒等関手$1_\cC,1_\cD$や恒等自然変換$1_F,1_G$については第2回の記事を，垂直合成$\c$と水平合成$\b$については第3回の記事をご参照ください。

単位$\eta \colon 1_\cC \nto G \b F$と余単位$\varepsilon \colon F \b G \nto 1_\cD$を，それぞれ次の図式の右辺のように表すことにします。

単位!FORMULA[15][1118736778][0]と余単位!FORMULA[16][1891918441][0] 単位$\eta$と余単位$\varepsilon$

ただし，図式では恒等関手$1_\cC$や$1_\cD$を表す線は省略しています（直観的には，恒等関手は「何もしない」関手であり，省略しても問題は生じません）。このとき，式\eqref{eq:1}は次式のように表されます。

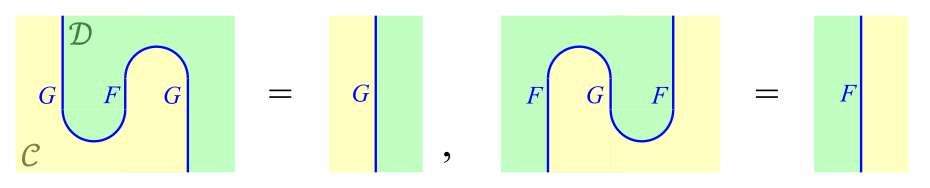ジグザグ等式 $$\tag{2}\label{eq:2}$$

なお，この式の1番左の式は$(1_G \b \varepsilon) \c (\eta \b 1_G)$を表していますが，このことは

!FORMULA[21][-503926258][0] $(1_G \b \varepsilon) \c (\eta \b 1_G)$

のように補助線を引いて4個の領域に分割すればわかりやすいと思います。左上・右上・左下・右下の領域がそれぞれ$1_G, ~\varepsilon, ~\eta, ~1_G$を表しており，これらの合成（水平合成・垂直合成）として$(1_G \b \varepsilon) \c (\eta \b 1_G)$を表しています。

式\eqref{eq:2}（と式\eqref{eq:1}）はジグザグ等式のようによばれます。この図式は，直観的には「ジグザグした（＝くねくねと曲がった）線は真っ直ぐに伸びた線に等しい」と解釈できます。

定義2：自然な可逆写像を用いた定義

定義1と同値な定義を紹介します。

随伴

関手$F \colon \cC \to \cD$と関手$G \colon \cD \to \cC$を考える。各$c \in \cC$と$d \in \cD$について次の可逆写像
$$ \varphi_{c,d} \colon \cD(Fc,d) \to \cC(c,Gd) $$ $$\tag{3}\label{eq:3}$$

が存在し，この写像の組$\varphi \coloneqq \{ \varphi_{c,d} \}_{c \in \cC, d \in \cD}$が任意の$f \in \cD(Fc,d), ~g \in \cC(c',c), ~h \in \cD(d,d')$に対して
$$ Gh \c \varphi_{c,d}(f) \c g = \varphi_{c',d'}(h \c f \c Fg) $$ $$\tag{4}\label{eq:4}$$
を満たすとき，組$\braket{F,G,\varphi}$を随伴とよぶ。

補足：

定義1では組$\braket{F,G,\eta,\varepsilon}$を随伴とよんでいるのに対し，定義2では組$\braket{F,G,\varphi}$を随伴とよんでいます。しかし，$\eta$と$\varepsilon$が与えられれば$\varphi$が定まり，逆も成り立つことがわかっていますので，実質的に同じものを表しています。

高度な話題：

詳しい説明は割愛しますが，関手$\cD(F\Endash,\Enndash)$と関手$\cC(\Endash,G\Enndash)$というものを用いれば，上の定義は「自然同型$\varphi \colon \cD(F\Endash,\Enndash) \cong \cC(\Endash,G\Enndash)$が存在するとき組$\braket{F,G,\varphi}$を随伴とよぶ」と言い換えられます。

式\eqref{eq:3}では，集合$\cD(Fc,d)$（つまり$Fc$から$d$への射の全体）と集合$\cC(c,Gd)$（つまり$c$から$Gd$への射の全体）の間には可逆写像があることを主張しています。また，式\eqref{eq:4}をすぐに理解することは困難かもしれませんが，この式はこれらの可逆写像の間に「自然な性質」が成り立っていることを主張しています。

定義1$\Rightarrow$定義2の導出

ここでは，定義1で定められた随伴$\braket{F,G,\eta,\varepsilon}$から定義2を満たす随伴$\braket{F,G,\varphi}$を導けることを示します。各$c \in \cC, ~d \in \cD$について，写像$\varphi_{c,d}$を

$$ \varphi_{c,d} \colon \cD(Fc,d) \ni f \mapsto Gf \c \eta_c \in \cC(c,Gd) $$

と定めます。図式で表すと次のようになります。

!FORMULA[56][715790010][0] $\varphi_{c,d}(f) = Gf \c \eta_c$

また，写像$\psi_{c,d}$を

$$ \psi_{c,d} \colon \cC(c,Gd) \ni g \mapsto \varepsilon_d \c Fg \in \cD(Fc,d) $$

と定めます。図式では次のように表されます。

!FORMULA[59][34364203][0] $\psi_{c,d}(g) = \varepsilon_d \c Fg$

このとき，$\psi_{c,d}$が$\varphi_{c,d}$の逆写像であることを容易に確認できます。実際，$\psi_{c,d} \c \varphi_{c,d}$が恒等写像であることは，各$f \in \cD(Fc,d)$について次式が成り立つことからわかります。

!FORMULA[64][-694922469][0]の証明 $\psi_{c,d}(\varphi_{c,d}(f)) = f$の証明

補助線で囲まれた箇所は$\varphi_{c,d}(f)$です。2行目の最初の等号では余単位$\varepsilon$を下に移動させており，最後の等号ではジグザグ等式（式\eqref{eq:2}）を用いています。

式\eqref{eq:4}が成り立つことは，次式からわかります（単位$\eta$を下に移動させているだけです）。

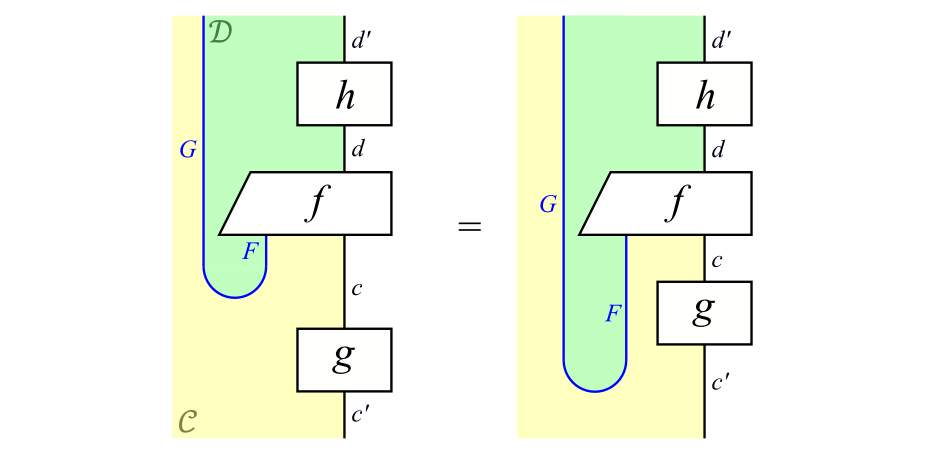$式\eqref{eq:4}$ 式\eqref{eq:4}

ここでは「定義1$\Rightarrow$定義2」を示しましたが，この逆も容易に示せます（拙著Nak-2025で説明しています）。

随伴が導くモナド

任意の随伴からモナドが得られることが知られています。

任意の随伴$\braket{F,G,\eta,\varepsilon}$について$\braket{G \b F,G \b \varepsilon \b F,\eta}$はモナドである。

このモナドは，随伴$\braket{F,G,\eta,\varepsilon}$が導くモナドとよばれます。

$F \colon \cC \to \cD$として，$T \coloneqq G \b F$および$\mu \coloneqq G \b \varepsilon \b F$とおく。$\mu$と$\eta$はそれぞれ次式のように表される。

!FORMULA[77][36095940][0]と!FORMULA[78][1118736778][0] $\mu$と$\eta$

なお，直観的には，これらの左辺における青線が右辺では太い線で表され，線の内側が緑色になっていると捉えるとわかりやすいかもしれない。次のように，図式を重ねて考えてもよいと思う。

!FORMULA[79][36095940][0]と!FORMULA[80][1118736778][0]の図式の直観的な解釈 $\mu$と$\eta$の図式の直観的な解釈

モナドの定義（第5回の記事を参照のこと）より，$\braket{T,\mu,\eta}$がモナドであることを示すためには，結合律と単位律が成り立つことを示せば十分である。結合律が成り立つことは次式からわかる。

結合律の証明

また，単位律が成り立つことは次式からわかる。

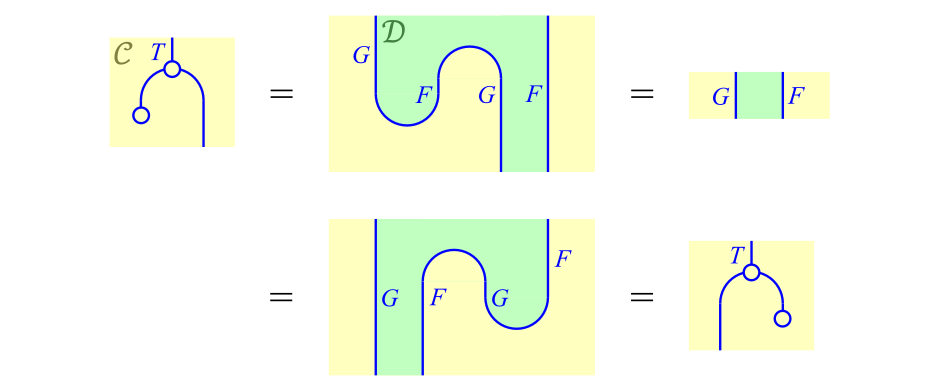単位律の証明

ただし，2番目と3番目の等号ではジグザグ等式（式\eqref{eq:2}）を用いた。

なお，この命題の逆として，任意のモナド$\braket{T,\mu,\eta}$はある随伴$\braket{F,G,\eta,\varepsilon}$が導くモナドになっていることが知られています（拙著Nak-2025で説明しています）。

随伴は圏同値の一般化

次の命題が示すように，2個の圏$\cC$と$\cD$が圏同値とよばれる関係にあれば，そこから随伴が得られます。この意味で，随伴は圏同値の一般化といえます。

圏同値は随伴を導く

2個の圏$\cC,\cD$について，2個の関手$F \colon \cC \to \cD, ~G \colon \cD \to \cC$と2個の自然同型$\eta \colon 1_\cC \cong G \b F, ~\tau \colon F \b G \cong 1_\cD$が存在するとする（この条件を満たすとき，$\cC$と$\cD$は同値であるとよぶ）。このとき，$\eta$を単位とするような随伴$\braket{F,G,\eta,\varepsilon}$が存在する。

自然変換$\varepsilon \colon F \b G \nto 1_\cD$を次のように定義する。

!FORMULA[94][1891918441][0] $\varepsilon$

このとき，随伴の定義1より$\eta$と$\varepsilon$がジグザグ等式（式\eqref{eq:2}）を満たすことを示せばよい。式\eqref{eq:2}の右側の等式が成り立つことは次式からわかる。

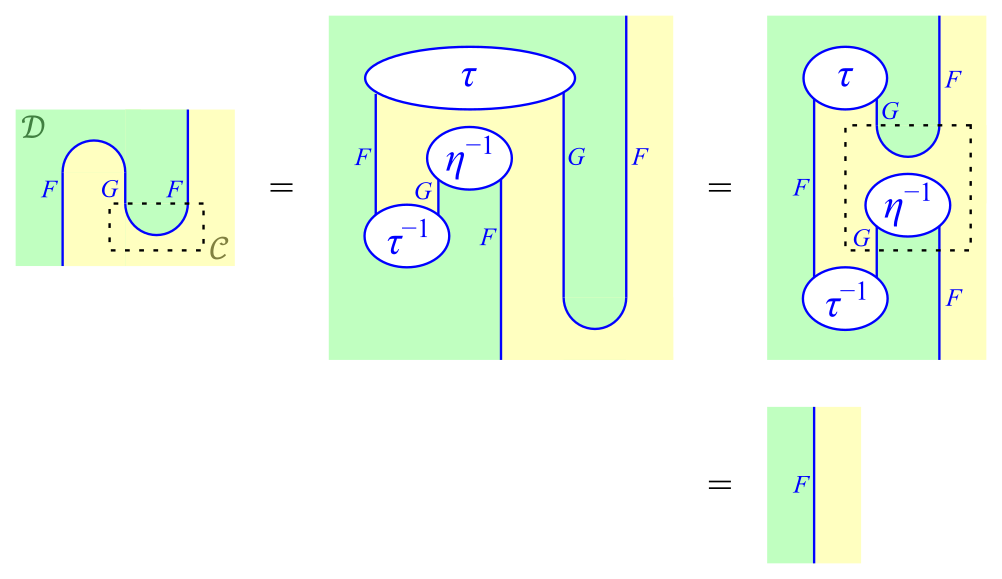$式\eqref{eq:2}の右側の等式の証明$ 式\eqref{eq:2}の右側の等式の証明

ただし，最初の式の補助線で囲まれた箇所は$\eta$を表している。また，

!FORMULA[98][1242830142][0] $\alpha$

が$1_G$に等しいことを示す。

!FORMULA[100][-874546976][0] $\alpha \c \alpha = \alpha$

が成り立つため，$\alpha \c \alpha = \alpha$である。一方，自然同型のみを合成して得られる自然同型は自然同型であり（証明は割愛），ここから$\varepsilon$は自然同型で，$\alpha$も同様に自然同型であることがわかる。したがって$\alpha^{-1}$が存在する。$\alpha \c \alpha = \alpha$の両辺に（左側または右側から）$\alpha^{-1}$を施せば$\alpha = 1_G$を得る。