【ストリング図で学ぶ圏論 #10】ホム関手のストリング図(前編)
はじめに
ホム関手は,圏論の各所で登場する非常に重要な関手です。この記事では,ホム関手に関連する図式を視覚的に表すための記法である「点線の枠による表記」を紹介します。この表記は,これまでの表記に似ているため扱いやすく,慣れると便利な場面がしばしばあります。「点線の枠による表記」は,米田の補題や普遍性,カン拡張などを直観的に理解する上で威力を発揮することになります。
本連載の目次
#1:
圏の定義と具体例
#2:
関手と自然変換
#3:
垂直合成と水平合成
#4:
モノイダル圏
#5:
モナドとは自己関手の圏におけるモノイド対象のこと
#6:
モナドの例
#7:
随伴
#8:
関手を表す線の順序の交換
#9:
普遍射と随伴・極限・カン拡張
#10: ホム関手のストリング図(前編)(この記事)
#11:
ホム関手のストリング図(後編)
#12:
米田の補題
番外編1:
視覚的に理解するクライスリトリプルとモナドの同値性
番外編2:
線形代数の圏論的な性質(?)を圏論なしで説明する
ホムセットやホム関手などのストリング図
ホムセット$\cC(c,a)$
任意の$c,a \in \cC$について,ホムセット$\cC(c,a)$を次の図式で表すことにします。
![集合!FORMULA[3][-250869181][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F9gPmhnufM9SMe5jSWnJV.png?alt=media) 集合$\cC(c,a)$
集合$\cC(c,a)$
左辺の点線の枠がホムセット$\cC(c,a)$を表しており,この点線の枠の中に$\cC(c,a)$の要素(つまり射)が入ると考えるとわかりやすいと思います。この最後の式が表すように,集合$\cC(c,a)$は集合の圏$\Set$( 第1回の記事 を参照のこと)の対象です。
このように点線の枠を含んだ図式を「点線の枠による表記」とよぶことにします。
写像$f \c \Endash \colon \cC(c,a) \to \cC(c,b)$
定義
任意の$c,a,b \in \cC$と$f \colon a \to b$について,写像
$$ \cC(c,a) \ni g \mapsto fg \in \cC(c,b) $$
を$(f \c \Endash)_c$(または添字$c$を省略して単に$f \c \Endash$)と書く。また,
$$ \cC(b,c) \ni h \mapsto hf \in \cC(a,c) $$
を$(\Endash \c f)_c$(または添字$c$を省略して単に$\Endash \c f$)と書く。
図式による表記
添字の情報を含んだ集まりを$\{ a_x \}_{x \in X}$のように表すことにします。$\{ a_x \}_{x \in X}$とは,添字$x \in X$と対応する値$a_x$との組$\braket{x,a_x}$(←これは$x$と$a_x$の組を表しています)の集まりのことだと考えてください。このとき,集まり$X$から集まり$Y$への写像$f \colon X \to Y$は,$X \ni x \mapsto f(x) \in Y$と表せますが,別の表記として$\{ f(x) \}_{x \in X}$とも表せます。以降では,このような表記を用います。
写像$(f \c \Endash)_c$を次の図式で表すことにします。
![写像!FORMULA[43][835659795][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FyHrgjGiNFaxalbXFVvqY.png?alt=media) 写像$(f \c \Endash)_c$
写像$(f \c \Endash)_c$
同様に,$(\Endash \c f)_c$を次の図式で表すことにします。
![写像!FORMULA[45][1506435793][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FOQQBriXEJbXDZTBAnPNB.png?alt=media) 写像$(\Endash \c f)_c$
写像$(\Endash \c f)_c$
これらの左辺の図式が「点線の枠による表記」です。これらの式の右辺が表すように,$(f \c \Endash)_c$は圏$\Set$の$\cC(c,a)$から$\cC(c,b)$への射であり,$(\Endash \c f)_c$は圏$\Set$の$\cC(b,c)$から$\cC(a,c)$への射です。
また,これらの式の左辺で示した表記のように,これまでの図式において一部のブロックを点線の枠で置き換えたものを,「その点線の枠に射を入力すると射を返すような写像」とみなすことにします。
ホム関手$\yoneda{c} = \cC(c,\Endash)$
定義
圏$\cC$から圏$\Set$への関手を$\cC$からの集合値関手とよびます。集合値関手のうち,$c \in \cC$に対応する関手が次のように定められます。
圏$\cC$の対象$c$を任意に選ぶ。$\cC$からの集合値関手のうち,「対象への作用」と「射への作用」が次のように与えられるものをホム関手とよび,$\cC(c,\Endash)$または$\yoneda{c}$と書く。
- [対象への作用] $\cC$の各対象$a$を$\Set$の対象(つまり集合)$\cC(c,a)$に写す。
- [射への作用] $\cC$の各射$f \colon a \to b$($a,b \in \cC$は任意)を$\Set$の射(つまり写像)$f \c \Endash \colon \cC(c,a) \to \cC(c,b)$に写す。
ホム関手$\yoneda{c}$が関手であることは,後で証明します。
図式による表記
ホム関手$\yoneda{c}$を次の図式で表すことにします。
![ホム関手!FORMULA[76][-1990610223][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F8LMoUiNG51kJLMN2i0xc.png?alt=media) ホム関手$\yoneda{c}$
ホム関手$\yoneda{c}$
$$\tag{1}\label{eq:yoneda_c}$$
この右側の図式が,ここで新たに導入する表記です。直観的には,この右辺の「$\Endash$」の箇所に$\cC$の対象や射が入ると解釈できます。実際,「$\Endash$」の箇所に対象が入ると考えると,$\yoneda{c}$の「対象への作用」が次式のように得られます(この右辺と式\eqref{eq:yoneda_c}の右辺を比べてみてください)。
![ホム関手!FORMULA[82][-1990610223][0]の「対象への作用」](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FJUSuwpko8FwlslhYgaSI.png?alt=media) ホム関手$\yoneda{c}$の「対象への作用」
ホム関手$\yoneda{c}$の「対象への作用」
また,「$\Endash$」の箇所に射が入ると考えると,$\yoneda{c}$の「射への作用」が次式のように得られます(この右辺と式\eqref{eq:yoneda_c}の右辺を比べてみてください)。
![ホム関手!FORMULA[85][-1990610223][0]の「射への作用」](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FtZqn7ydaH0ke5JNoirNy.png?alt=media) ホム関手$\yoneda{c}$の「射への作用」
ホム関手$\yoneda{c}$の「射への作用」
関手であることの証明
任意の$c \in \cC$について,ホム関手$\yoneda{c}$は関手である。
$\yoneda{c}$が関手であることを証明する。このためには,結合律を保って恒等射を恒等射に写すことを示せば十分である。
まず,結合律を保つ,つまり任意の$f \in \cC(x,y)$と$g \in \cC(y,z)$($x,y,z \in \cC$も任意)に対して$\yoneda{c}(gf) = \yoneda{c}(g) \c \yoneda{c}(f)$が成り立つことを示す。このことは,次式からわかる。
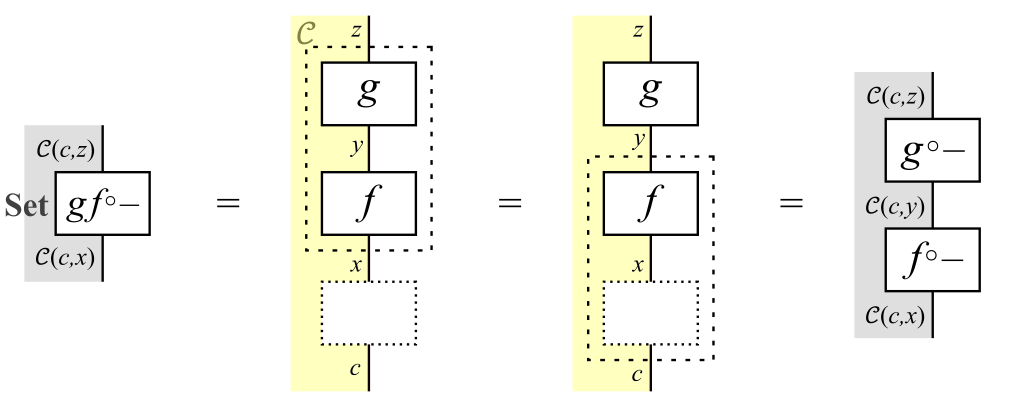 結合律を保つことの証明
結合律を保つことの証明
次に,恒等射を恒等射に写す,つまり各$x \in \cC$に対して$\yoneda{c}(1_x)$が恒等射であることを示す。このことは,次式からわかる。
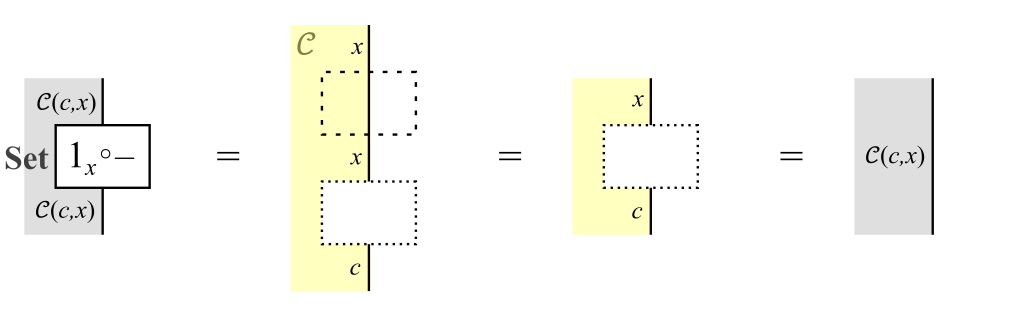 恒等射を恒等射に写すことの証明
恒等射を恒等射に写すことの証明
ただし,補助線で囲まれた領域は$1_x$である。したがって,$\yoneda{c}(1_x)$は恒等射$1_{\cC(c,x)}$に等しい。
ホム関手$\yoneda{c}$を点線の枠による表記を用いて表すことに慣れると,この証明で現れた図式の等号が成り立つことは明らかだと感じるようになると思います。
自然変換$\yoneda{p} \colon \yoneda{d} \nto \yoneda{c}$
定義
対象$c \in \cC$に対応するホム関手$\yoneda{c}$が定められました。同様に,射$p \in \cC(c,d)$に対応する自然変換$\yoneda{p} \colon \yoneda{d} \nto \yoneda{c}$を次のように定められます。
圏$\cC$の対象$c,d$と射$p \in \cC(c,d)$を任意に選ぶ。$\yoneda{d}$から$\yoneda{c}$への自然変換のうち,対象への作用が次のように与えられるものを$\yoneda{p}$と書く。
- [対象への作用] $\cC$の各対象$a$を$\Set$の射(つまり写像)$\Endash \c p \colon \cC(d,a) \to \cC(c,a)$に写す。
- [射への作用] $\cC$の各射$f \colon a \to b$を$\Set$の射(つまり写像)$f \c \Endash \c p \colon \cC(d,a) \ni h \mapsto fhp \in \cC(c,b)$に写す。
$\yoneda{p}$が自然変換であることは,後で証明します。
図式による表記
自然変換$\yoneda{p}$を次の図式で表すことにします。
![自然変換!FORMULA[131][-1990597730][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FMBJfhB6zuMLlgB3VjJkD.png?alt=media) 自然変換$\yoneda{p}$
自然変換$\yoneda{p}$
$\yoneda{p}$は,次のようなブロックでも表せます。
![自然変換!FORMULA[133][-1990597730][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FVXJwuqs9ezEVhWjh4yVI.png?alt=media) 自然変換$\yoneda{p}$
自然変換$\yoneda{p}$
ホム関手$\yoneda{c}$の場合と同様に,直観的には,この右辺の「$\Endash$」の箇所に$\cC$の対象や射が入ると解釈できます。実際,「$\Endash$」の箇所に対象が入ると考えると,$\yoneda{p}$の「対象への作用」が次式のように得られます。
![自然変換!FORMULA[139][-1990597730][0]の「対象への作用」](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FQYPgwehfYmlwhTB1FjLz.png?alt=media) 自然変換$\yoneda{p}$の「対象への作用」
自然変換$\yoneda{p}$の「対象への作用」
また,「$\Endash$」の箇所に射が入ると考えると,$\yoneda{p}$の「射への作用」が次式のように得られます。
![自然変換!FORMULA[142][-1990597730][0]の「射への作用」](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FWUg28a1uWYWowKv9YS58.png?alt=media) 自然変換$\yoneda{p}$の「射への作用」
自然変換$\yoneda{p}$の「射への作用」
自然変換であることの証明
任意の$p \in \cC(c,d)$($c,d$も任意)について,$\yoneda{p}$は自然変換である。
$\yoneda{p}$が自然性を満たすことを示せばよく,これは任意の$f \in \cC(a,b)$について次式が成り立つことからわかる。
![!FORMULA[148][-1990597730][0]の自然性の証明](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FgB7QXePXBhp7mRV2bmbu.png?alt=media) $\yoneda{p}$の自然性の証明
$\yoneda{p}$の自然性の証明
ホム関手$\yoneda{c}$の場合と同様に,$\yoneda{p}$を点線の枠を用いた式として表すことに慣れると,$\yoneda{p}$が自然性を満たすことは明らかだと感じるようになると思います。点線の枠を用いて表せるようなほかの自然変換に対しても,それが自然性を満たすことを容易に確認できます。
まとめ
(A)ホムセット$\cC(c,a)$,(B)射$f \c \Endash$,(C)ホム関手$\yoneda{c}$,(D)自然変換$\yoneda{p}$を,点線の枠による表記を用いて次式のように表す方法を紹介しました。
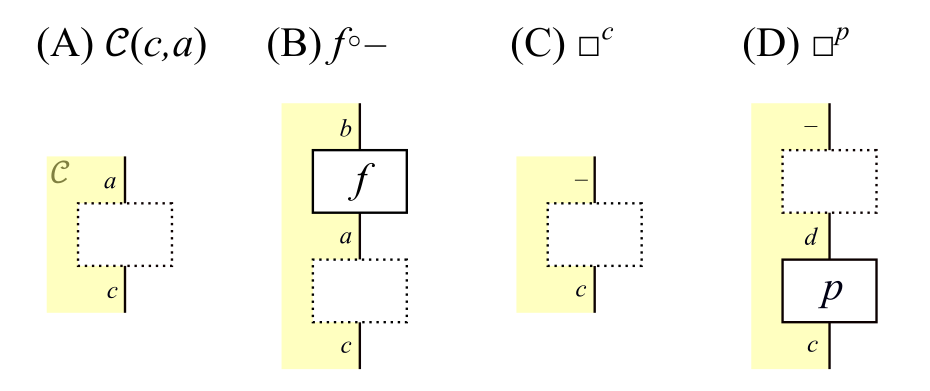 まとめ
まとめ
(B)の図式は,「点線の枠に$\cC$の射$h$を入力すると$\cC$の射$fh$を返すような写像」と解釈できます。また,$\cC(c,a)$を$1_{\cC(c,a)}$と同一視すれば,(A)の図式も同じ解釈(つまり,「点線の枠に$\cC$の射$h$を入力すると$h$自身を返すような写像」という解釈)ができます。
(C)と(D)の図式は,線$\Endash$に$\cC$の対象が入ると考えると「対象への作用」と解釈できて,線$\Endash$に$\cC$の射が入ると考えると「射への作用」と解釈できます。$\yoneda{c}$が関手で$\yoneda{p}$が自然変換であることは,これらの図式に慣れれば自明だと感じられるようになると思います。実際,これらの証明を振り返ると,「$\yoneda{c}$が関手で$\yoneda{p}$が自然変換であるという情報を,点線の枠による表記では自明な形で表せている」といっても過言ではないと思います。
