【ストリング図で学ぶ圏論 番外編1】視覚的に理解するクライスリトリプルとモナドの同値性
はじめに
クライスリトリプルは,計算機科学などの分野で(たとえばHaskellなどの関数型プログラミング言語において)しばしば登場する概念です。クライスリトリプルはモナドと密接に関連しており,ストリング図に慣れればこれらの関係を視覚的にわかりやすい形で表すことができます。
この記事では,クライスリトリプルについて説明した後で,モナドとの関係をストリング図により示します。なお,この記事は圏論に不慣れな方でも大まかな雰囲気がつかめることをめざして書いています。
本連載の目次
#1:
圏の定義と具体例
#2:
関手と自然変換
#3:
垂直合成と水平合成
#4:
モノイダル圏
#5:
モナドとは自己関手の圏におけるモノイド対象のこと
#6:
モナドの例
#7:
随伴
#8:
関手を表す線の順序の交換
#9:
普遍射と随伴・極限・カン拡張
#10:
ホム関手のストリング図(前編)
#11:
ホム関手のストリング図(後編)
#12:
米田の補題
番外編1: 視覚的に理解するクライスリトリプルとモナドの同値性(この記事)
番外編2:
線形代数の圏論的な性質(?)を圏論なしで説明する
クライスリトリプル
クライスリトリプルの定義
まず,クライスリトリプルの定義を示します。以降では,圏の定義は知っているものとします。$a$が圏$\cC$の対象であることを$a \in \cC$と表し,また各$a,b \in \cC$について$\cC$の$a$から$b$への射全体からなる集まりを$\cC(a,b)$と表します。$\cC$の対象全体からなる集まりを$\ob \cC$と表します。
$\cC$を圏とし,次の三つ組を考える。
(a) 写像$T \colon \ob \cC \to \ob \cC$
(b) 射の集まり$\eta \coloneqq \{ \eta_a \in \cC(a,Ta) \}_{a \in \cC}$($\eta$を単位元とよぶ)
(c) 写像の集まり$\Endash^\# \coloneqq \{\Endash^\#_{a,b} \colon \cC(a,Tb) \to \cC(Ta,Tb)\}_{a,b \in \cC}$($\Endash^\#$や$\Endash^\#_{a,b}$を持ち上げとよぶ)
各$f \in \cC(a,Tb)$に対して,$\Endash^\#_{a,b}(f) \in \cC(Ta,Tb)$を$f^\#$と書くことにする($f$の持ち上げとよぶ)。任意の$a,b,c \in \cC$と$f \in \cC(a,Tb)$ と$g \in \cC(b,Tc)$に対して次の三つの条件が成り立つとき,この三つ組$\braket{T,\eta,\Endash^\#}$をクライスリトリプルとよぶ。
(1) $(g^\# \c f)^\# = g^\# \c f^\#$
(2) $\eta_a^\# = 1_{Ta}$
(3) $f^\# \c \eta_a = f$
なお,$\c$ は射の合成を表す。
Monad は,return関数とバインド関数により定められます。この Monad は,クライスリトリプルのことだと考えるとわかりやすいと思います。具体的には,上の定義における単位元$\eta$はreturn関数のことであり,持ち上げ$\Endash^\#$はバインド関数 >>= に対応しています($f^\#(m)$が m >>= f で表されます)。上の三つの条件は,次のように書き換えられます。(1)
m >>= (\x -> f x >>= g) == (m >>= f) >>= g(2)
m >>= return == m(3)
(return x) >>= f == f x$T$は関手で$\eta$は自然変換
クライスリトリプルの定義から,$T$は$\cC$から$\cC$への関手であり,$\eta$は$1_\cC$から$T$への自然変換であることがわかります。念のため,このことを確認しておきます。
これらを確認する作業はやや退屈かと思いますので,この作業に興味のない方(または関手・自然変換に不慣れな方)は読み飛ばしても構いません。
$T$は関手
各$f \in \cC(a,b)$($a,b \in \cC$は任意)に対して
$$ Tf \coloneqq (\eta_b \c f)^\# $$ $$\tag{1}\label{eq:T}$$
と定めます。このとき,$T$が関手であることを示すためには,合成を保存して,恒等射を恒等射に写すことを示せば十分です。合成を保存することは,各$f \in \cC(a,b),~g \in \cC(b,c)$に対して
$$ T(g \c f) \overset{\text{式\eqref{eq:T}}}{=} (\eta_c \c g \c f)^\# \overset{\text{条件(3)}}{=} ((\eta_c \c g)^\# \c \eta_b \c f)^\# \overset{\text{条件(1)}}{=} (\eta_c \c g)^\# \c (\eta_b \c f)^\# \overset{\text{式\eqref{eq:T}}}{=} Tg \c Tf $$
が成り立つことからわかります。恒等射を恒等射に写すことは,各$a \in \cC$に対して
$$ T(1_a) \overset{\text{式\eqref{eq:T}}}{=} (\eta_a \c 1_a)^\# = \eta_a^\# \overset{\text{条件(2)}}{=} 1_{Ta} $$
が成り立つことからわかります。
$\eta$は自然変換
各$f \in \cC(a,b)$に対して
$$ Tf \c \eta_a \overset{\text{式\eqref{eq:T}}}{=} (\eta_b \c f)^\# \c \eta_a \overset{\text{条件(3)}}{=} \eta_b \c f $$
が成り立ちます。つまり,$\eta$は自然性を満たします。したがって,$\eta$は($1_\cC$から$T$への)自然変換です。
クライスリトリプルを表す図式
リストモナドの例
一般的な場合について述べる前に,具体例として 第6回の記事 で述べたリストモナド$L$を考えることにします(Haskellをご存知の方は,お馴染みのリストモナドをイメージしてください)。各集合$X$に対して,$LX$は「$X$の要素からなる有限長のリスト」の集合を表します。$LX$の各要素は$\braket{x_i}_i \coloneqq \braket{x_1,x_2,\dots}$(ただし$x_1,x_2,\dots \in X$)の形で表され,この要素は次の図式で表されます。
![!FORMULA[89][-1011194683][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FWyBJ7YNzs2k6ZzHhv33x.png?alt=media) $\braket{x_i}_i$
$\braket{x_i}_i$
四角いブロックが$\braket{x_i}_i$を表しています。また,このブロックの上側に2本の線$L$と$X$を描くことで,$\braket{x_i}_i$が$LX$の要素であることを表しています。
各集合$X$に対し,$\eta_X$は集合$X$の各要素$x$を長さ1のリスト$\braket{x} \in LX$に写す写像です。$\eta_X(x) = \braket{x}$は次式で表されます。
![!FORMULA[101][-2058486356][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FzNY1jQ1ujEwqNqIrpF3F.png?alt=media) $\eta_X(x) = \braket{x}$
$\eta_X(x) = \braket{x}$
青丸が$\eta$を表しており,左辺の補助線(破線)で囲まれた箇所が$\eta_X$を表しています。左辺では,$\eta_X$と$x$を縦方向につなげることで$\eta_X(x)$を表しています。
![!FORMULA[110][1126156845][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FHJyc0bRaExp61qqEz5vx.png?alt=media) $f(x)$
$f(x)$
このように,ブロック$f$の下側に線$X$をつなげて上側に2本の線$L$と$Y$をつなげることで,$f$が$X$から$LY$への写像であることを表します。また,2個のブロック$f$と$x$を縦方向につなげることで,$f(x)$を表します。この$f$に$\eta_X$を代入すると,先ほど示した$\eta_X(x)$の図式が得られます。
$f$の持ち上げ$f^\#$を次の図式で表すことにします。
![!FORMULA[126][37794][0]の持ち上げ!FORMULA[127][1127738465][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FnAZrqig6dYITwLKclBWg.png?alt=media) $f$の持ち上げ$f^\#$
$f$の持ち上げ$f^\#$
この図式にある青丸は,$\eta$を表す青丸とは似て非なるものだと考えてください。実際,こちらの青丸では,その下側から2本の青線が伸びています(上側からは1本の青線が伸びていますので,青丸から計3本の線が伸びています)。線はすべて関手$L$を表しています(線のラベル「$L$」は適宜省略しています)。
$f^\#$に要素$\braket{x_i}_i \in LX$を入力して得られる値$f^\#(\braket{x_i}_i) \in LY$は,次式で表されます。
![!FORMULA[134][-1131184421][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fjthm5gAmRjj5GjtXs5rx.png?alt=media) $f^\#(\braket{x_i}_i)$
$f^\#(\braket{x_i}_i)$
$f(x)$の場合と同様に,2個のブロック$f^\#$と$\braket{x_i}_i$を縦方向につなげることで$f^\#(\braket{x_i}_i)$を表しています。
単位元と持ち上げの図式
上で述べたリストモナドの図式を一般化して,単位元と持ち上げの図式を導入します。各$a \in \cC$に対し,$\eta_a$を次式で表すことにします。
![!FORMULA[141][1364279400][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FpHWaQaRbfSOIPZtlRHYR.png?alt=media) $\eta_a$
$\eta_a$
図式では,関手$T$を青線で描きます。また,青丸は自然変換$\eta$を表しており,青丸の右側に線$a$を描くことで$\eta_a$を表します。
各$a,b \in \cC$に対し,持ち上げ$\Endash_{a,b}^\#$(つまり写像$\cC(a,Tb) \ni f \mapsto f^\# \in \cC(Ta,Tb)$)を次の図式で表すことにします。
![持ち上げ!FORMULA[149][-1670043148][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FklvpedlAAjyFVQH3dBhs.png?alt=media) 持ち上げ$\Endash_{a,b}^\#$
持ち上げ$\Endash_{a,b}^\#$
矢印$\mapsto$の左側および右側の図式が,それぞれ$f$および$f^\#$を表しています。なお,リストモナドの場合と同様に,この図式にある青丸は$\eta$を表す青丸とは似て非なるものだと考えてください。線はすべて関手$T$を表しています。
なお,持ち上げ$\Endash_{a,b}^\#$は次式のようにも表せます。
![持ち上げ!FORMULA[156][-1670043148][0]の別表現](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FBUk4QLWt6VAh2hiZAxQe.png?alt=media) 持ち上げ$\Endash_{a,b}^\#$の別表現
持ち上げ$\Endash_{a,b}^\#$の別表現
この図式では,点線の枠の中に$f$を入力すると$f^\#$を表す図式が得られますので,写像$f \mapsto f^\#$を表しているものと解釈します。この解釈により,この写像は持ち上げ$\Endash_{a,b}^\#$を表していることがわかります。
![!FORMULA[166][-1460886842][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FR474512hAHsCBUtDmVlc.png?alt=media) $1_{Ta}^\#$
$1_{Ta}^\#$
念のため,$\mu$が$T \b T$から$T$への自然変換である,つまり各$f \in \cC(a,b)$に対して$Tf \c 1_{Ta}^\# = 1_{Tb}^\# \c T(Tf)$を満たすことを確認しておきます(ただし,$\b$は水平合成)。この左辺は
$$ Tf \c 1_{Ta}^\# \overset{\text{条件(1)}}{=} (Tf \c 1_{Ta})^\# = (Tf)^\# $$
であり(最初の等号では,式\eqref{eq:T}より$Tf$が$\eta_b \c f$の持ち上げに等しいことを用いた),右辺は
$$ 1_{Tb}^\# \c T(Tf) \overset{\text{式\eqref{eq:T}}}{=} 1_{Tb}^\# \c (\eta_{Tb} \c Tf)^\# \overset{\text{条件(1)}}{=} (1_{Tb}^\# \c \eta_{Tb} \c Tf)^\# \overset{\text{条件(3)}}{=} (1_{Tb} \c Tf)^\# = (Tf)^\# $$
ですので,左辺と右辺は同じです。
クライスリトリプルとモナドの関係
以降では,クライスリトリプルとモナドの関係について述べます。
モナドの定義
まず,モナドの定義を述べておきます( 第5回の記事 で述べたものと同じです)。
関手$T \colon \cC \to \cC$と自然変換$\eta \colon 1_\cC \nto T$(単位元とよぶ)と自然変換$\mu \colon T \b T \nto T$(積とよぶ)の組$\braket{T,\eta,\mu}$が次の二つの条件を満たすとき,モナドとよぶ。
(1')結合律:$\mu \c (1_T \b \mu) = \mu \c (\mu \b 1_T)$
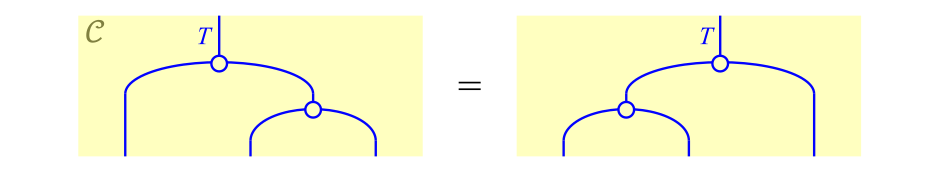 結合律
$$\tag{1}\label{eq:association}$$
結合律
$$\tag{1}\label{eq:association}$$
ただし,3本の線がつながった青丸は$\mu$を表している。また,$\b$は水平合成を表している。
(2')単位律:$\mu \c (1_T \b \eta) = 1_T = \mu \c (\eta \b 1_T)$
 単位律
$$\tag{2}\label{eq:unit}$$
単位律
$$\tag{2}\label{eq:unit}$$
ただし,1本の線がつながった青丸は$\eta$を表している。
![!FORMULA[191][218819630][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FQo56qYuUX2fj7xtWrNpH.png?alt=media) $\mu \c (1_T \b \mu)$
$\mu \c (1_T \b \mu)$
のように補助線で区切るとわかりやすいと思います。補助線で区切られた3個の領域が,それぞれ$\mu$(上側),$1_T$(左下側),$\mu$(右下側)を表しています。$1_T$(左下側)と$\mu$(右下側)を横につなげることで$1_T \b \mu$が得られ,これに$\mu$(上側)をつなげることで$\mu \c (1_T \b \mu)$が得られます。
クライスリトリプルとモナドの同値性
任意のクライスリトリプルから対応するモナドを構成できて,逆に任意のモナドから対応するクライスリトリプルを構成できることが知られています。このような意味で,クライスリトリプルとモナドは同一視できます。この記事では,このような関係を同値性とよんでいます。
この同値性は,「クライスリトリプルの定義(Kleisli)で述べた三つの条件」が「モナドの定義(Monad)で述べた二つの条件(つまり結合律と単位律)」に対応していることから示せます。また,この対応は,図式を用いれば素直に理解できると思います。以降では,前者の三つの条件を図式で表すことで,このことを示します。
条件(1):$(g^\# \c f)^\# = g^\# \c f^\#$
条件(1)は次の図式で表せます。
![条件(1)(!FORMULA[201][-262603950][0])](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FGQpM0kqhl90d7tI0LRLs.png?alt=media) 条件(1)($(g^\# \c f)^\# = g^\# \c f^\#$)
条件(1)($(g^\# \c f)^\# = g^\# \c f^\#$)
この左辺では,補助線で囲まれた領域が$g^\# \c f$を表しており,左辺全体でその持ち上げ,つまり$(g^\# \c f)^\#$を表しています。また,右辺では,$g^\#$を表す図式と$f^\#$を表す図式を縦方向につなげています(なお,射の合成$\c$が縦方向につなげることを意味します)。
この右辺を変形して青丸の位置を上のほうに動かすと,次の図式が得られます。なお,先ほどの図式に対し,右辺のみを変形しています(補助線はひとまず無視してください)。
![条件(1)(!FORMULA[207][-262603950][0])の別表現](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FkZ40x9ymOzWXQmthMFBy.png?alt=media) 条件(1)($(g^\# \c f)^\# = g^\# \c f^\#$)の別表現
$$\tag{3}\label{eq:cond1b}$$
条件(1)($(g^\# \c f)^\# = g^\# \c f^\#$)の別表現
$$\tag{3}\label{eq:cond1b}$$
式\eqref{eq:cond1b}が任意の$f$と$g$について成り立つことから,その左辺および右辺の補助線で囲まれた箇所が同じである,つまり
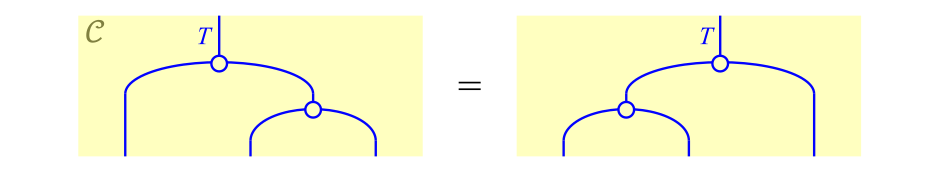 結合律
$$\tag{4}\label{eq:association2}$$
結合律
$$\tag{4}\label{eq:association2}$$
が成り立つことが容易に想像できます。この式は,式\eqref{eq:association}にほかなりません。このような関係を用いると,この条件(1)はモナドの定義(Monad)における結合律と同値であることが容易にわかります。
条件(2):$\eta_a^\# = 1_{Ta}$
条件(2)は次の図式で表せます。
![条件(2)(!FORMULA[223][1379147559][0])](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FldGPSPyIFnsxk6wMTsRL.png?alt=media) 条件(2)($\eta_a^\# = 1_{Ta}$)
条件(2)($\eta_a^\# = 1_{Ta}$)
この式が任意の$a \in \cC$について成り立つため,

が成り立ちます。この式は,式\eqref{eq:unit}の左側の等号にほかなりません。
条件(3):$f^\# \c \eta_a = f$
条件(3)は次の図式で表せます。
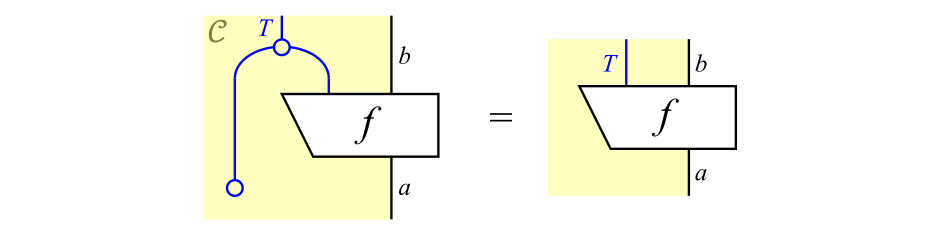 画像の名前
画像の名前
なお,この左辺では$f^\#$を表す図式と$\eta_a$を表す図式を縦方向につなげています。この左辺を変形して青丸$\eta$の位置を上のほうに動かすと,次の図式が得られます。
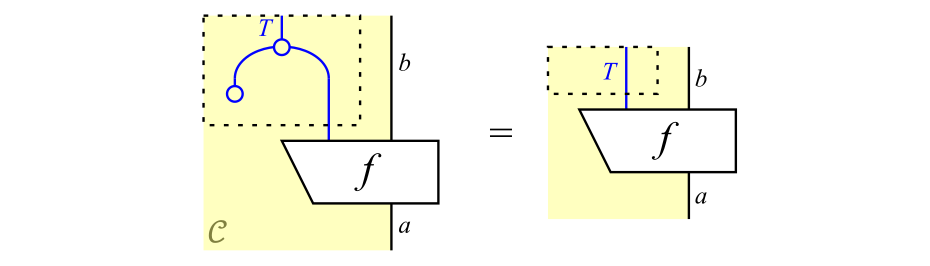 画像の名前
$$\tag{5}\label{eq:unit2a}$$
画像の名前
$$\tag{5}\label{eq:unit2a}$$
この式が任意の$f$について成り立つことから,その左辺および右辺の補助線で囲まれた箇所が同じである,つまり
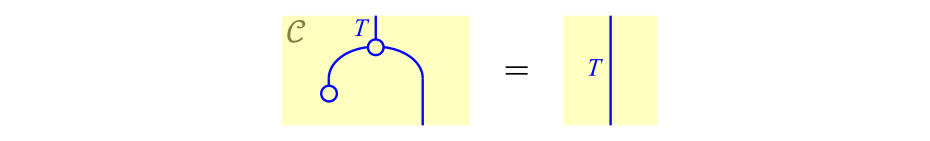 画像の名前
$$\tag{6}\label{eq:unit2b}$$
画像の名前
$$\tag{6}\label{eq:unit2b}$$
が成り立つことが容易に想像できます。この式は,式\eqref{eq:unit}の右側の等号にほかなりません。
以上により,条件(1)がモナドの定義(Monad)における結合律と同値であり,条件(2)と条件(3)が単位律と同値であることがわかります。
まとめ
ストリング図を用いると,クライスリトリプルとモナドの同値性を視覚的に理解できることを示しました。計算機科学などの分野において現れるモナドに関するほかの多くの性質も,このようなストリング図を用いると素直に表せることがわかります。その基本的なものは拙著Nak-2025の4.4節などで述べていますので,興味のある方はご参照ください。また,同じストリング図によりデータの流れを直観的な形で表せますので,ストリング図が描けるようになると便利かと思います。
