【ストリング図で学ぶ圏論 #12】米田の補題
はじめに
米田の補題は,圏論における非常に重要な命題です。この命題は,次のように述べられます。
任意の集合値関手$X \colon \cC \to \Set$と任意の対象$c \in \cC$について,$\Func{\cC}{\Set}(\yoneda{c},X) \cong Xc$である。
ここで,$\yoneda{c}$はホム関手$\cC(c,\Endash)$のことで,$\Func{\cC}{\Set}(\yoneda{c},X)$は$\yoneda{c}$から$X$への自然変換をすべて集めた集合です($\Func{\cC}{\Set}$は 第3回の記事 で述べた関手圏です)。また,$Xc$も集合です。このため,この命題は$\yoneda{c}$から$X$への各自然変換を集合$Xc$の要素に写すような可逆写像(つまり全単射)があることを主張しています。
以降では, 第10回 と 第11回 の記事で紹介した「点線の枠による表記」を用いて,この補題を視覚的にわかりやすい形で証明します。
なお,同型$\Func{\cC}{\Set}(\yoneda{c},X) \cong Xc$は$X$と$c$について自然でもあり,一般的に米田の補題とよんだ場合にはこの自然性も含まれます。この自然性については,あとで証明します。
本連載の目次
#1:
圏の定義と具体例
#2:
関手と自然変換
#3:
垂直合成と水平合成
#4:
モノイダル圏
#5:
モナドとは自己関手の圏におけるモノイド対象のこと
#6:
モナドの例
#7:
随伴
#8:
関手を表す線の順序の交換
#9:
普遍射と随伴・極限・カン拡張
#10:
ホム関手のストリング図(前編)
#11:
ホム関手のストリング図(後編)
#12: 米田の補題(この記事)
番外編1:
視覚的に理解するクライスリトリプルとモナドの同値性
番外編2:
線形代数の圏論的な性質(?)を圏論なしで説明する
準備
第1回の記事 で述べたように,任意の集合$X$について,各$x \in X$と写像$\{*\} \ni * \mapsto x \in X$(ただし$\{*\}$は1点集合)を同一視することにします。
ホム関手$\yoneda{c}=\cC(c,\Endash)$は$\cC$の各恒等射$1_d$を恒等写像$1_{\cC(c,d)}$に写します。この恒等写像は次式のように表せます。
![恒等写像!FORMULA[24][257973514][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FDD69uAi4gUZaRmwXOGrw.png?alt=media) 恒等写像$1_{\cC(c,d)}$
恒等写像$1_{\cC(c,d)}$
$$\tag{1}\label{eq:1}$$
ただし,右辺の黒丸は写像$\{*\} \ni * \mapsto 1_c \in \cC(c,c)$を表しており,これは上で述べた同一視により恒等射$1_c$のことです。実際に確認すると,左辺は$\yoneda{c}(1_d)$,つまり恒等写像$1_{\cC(c,d)}$を表しています。また,右辺は写像
$$ \cC(c,d) \ni f \mapsto \yoneda{c}(f) \c 1_c \in \Set(\{*\},\cC(c,d)) $$
を表しています。なぜならば,この右辺の点線の枠に各$f \in \cC(c,d)$を入力すると図式全体として$\yoneda{c}(f) \c 1_c$を表すためです。一方,$\yoneda{c}(f) \c 1_c$は写像$\yoneda{c}(f) = f \c \Endash$に$1_c$を代入したもの,つまり$f \c 1_c$に等しいため,$f$です。したがって,式\eqref{eq:1}の右辺は写像$f \mapsto f$を表しており,これは恒等写像$1_{\cC(c,d)}$にほかなりません。
自然変換$\tau \colon \yoneda{c} \nto X$を任意に選んだとき,式\eqref{eq:1}を用いると$\tau$の各成分$\tau_d$は次のように表されます。
![!FORMULA[43][1776765679][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FtqonNZSSjmbXD4k7s7X5.png?alt=media) $\tau_d$
$\tau_d$
$$\tag{2}\label{eq:2}$$
このため,$\tau$は次のように表されます。
![!FORMULA[46][1119166004][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F3uM8va4W9QMQID26ZLPi.png?alt=media) $\tau$
$\tau$
実際,この右辺の線$\Endash$を各線$d \in \cC$に置き換えると式\eqref{eq:2}の$\tau_d$に等しくなるため,右辺は自然変換$\tau$を表しています。
命題1の証明
では,米田の補題を証明します。
写像$\alpha_{X,c}$と写像$\beta_{X,c}$
まず,写像$\alpha_{X,c} \colon \Func{\cC}{\Set}(\yoneda{c},X) \to Xc$を次のように定めます。
![写像!FORMULA[54][630457012][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FYqCi79ePsIi2cs8DNBK3.png?alt=media) 写像$\alpha_{X,c}$
写像$\alpha_{X,c}$
この写像は,米田写像とよばれます。
また,写像$\beta_{X,c} \colon Xc \to \Func{\cC}{\Set}(\yoneda{c},X)$を次のように定めます。
![写像!FORMULA[59][-1302307470][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FS4UZKnIbUnuUNCjJ6lWi.png?alt=media) 写像$\beta_{X,c}$
写像$\beta_{X,c}$
$$\tag{3}\label{eq:3}$$
このとき,$\Func{\cC}{\Set}(\yoneda{c},X) \cong Xc$を示すためには$\beta_{X,c}$が$\alpha_{X,c}$の逆写像であることを示せば十分です。以下,これを示します。
$\beta_{X,c} = \alpha_{X,c}^{-1}$の証明
まず,$\beta_{X,c} \c \alpha_{X,c}$が恒等写像であることを示します。このことは次式からわかります。
![!FORMULA[71][-1083805459][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FlOZCt3hvLC0TA1Qykua8.png?alt=media) $\beta_{X,c} \c \alpha_{X,c}$
$\beta_{X,c} \c \alpha_{X,c}$
次に,$\alpha_{X,c} \c \beta_{X,c}$が恒等写像であることを示します。このことは次式からわかります。
![!FORMULA[73][1407431319][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FXQET4C5Daf6yoLIVn7l4.png?alt=media) $\alpha_{X,c} \c \beta_{X,c}$
$\alpha_{X,c} \c \beta_{X,c}$
したがって,$\beta_{X,c}$は$\alpha_{X,c}$の逆写像です。
応用例:行列の圏
第1回の記事 で述べた行列を射とする圏$\mathbf{Mat}$において,米田の補題を考えます。$\mathbf{Mat}$の対象の集合を$\cN$とおきます。このとき,任意の集合値関手$X \colon \mathbf{Mat} \to \Set$と任意の自然数$n \in \cN$について,
$$ \Func{\mathbf{Mat}}{\Set}(\yoneda{n},X) \cong Xn $$
が成り立ちます。なお,関手$\yoneda{n}$は次のような関手です。
- 各$k \in \cN$を集合$\mathbf{Mat}(n,k)$(つまり$k$行$n$列の行列全体)に写す。
- $k'$行$k$列の各行列$Z \in \mathbf{Mat}(k,k')$を写像$Z \c \Endash \colon \mathbf{Mat}(n,k) \ni A \mapsto ZA \in \mathbf{Mat}(n,k')$に写す。
とくに$X = \yoneda{m}$(ただし$m \in \cN$)の場合には,
$$ \Func{\mathbf{Mat}}{\Set}(\yoneda{n},\yoneda{m}) \cong \yoneda{m}(n) = \mathbf{Mat}(m,n) $$
が成り立ちます。このとき,可逆写像$\varphi_{m,n} \coloneqq \beta_{\yoneda{m},n}$は写像
$$
\mathbf{Mat}(m,n) \ni X \mapsto \yoneda{X} \in \Func{\mathbf{Mat}}{\Set}(\yoneda{n},\yoneda{m})
$$
$$\tag{4}\label{eq:4}$$
に等しいことを示せます。ただし,自然変換$\yoneda{X}$は 第10回の記事 で述べた自然変換$\yoneda{p}$に$p = X$を代入したものです。これは,関手$\yoneda{n}$から関手$\yoneda{m}$への自然変換と$n$行$m$列の行列が一対一に対応することを主張しています。また,$\yoneda{n}$から$\yoneda{m}$への自然変換は$\yoneda{X}$ $(X \in \mathbf{Mat}(m,n))$の形で表されるものに限られることも主張しています。
以降では,写像$\varphi_{m,n}$が式\eqref{eq:4}の写像に等しいことを確認しておきます。$n$行$m$列の各行列$X \in \mathbf{Mat}(m,n)$について,式\eqref{eq:3}より
![!FORMULA[112][-1069751337][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FRV0mlQpFvdlHwfj9v7cG.png?alt=media) $\varphi_{m,n}(X)$
$\varphi_{m,n}(X)$
が成り立ちます(なお,$X$は$\mathbf{Mat}(m,n) = \Set(\{*\},\mathbf{Mat}(m,n)) = \Set(\{*\},\yoneda{m}(n))$の要素です)。この右辺は$\yoneda{X}$にほかなりません。$\yoneda{X}$の各成分$\yoneda{X}{}_k$ $(k \in \cN)$は写像
$$ \Endash \c X \colon \mathbf{Mat}(n,k) \ni Z \mapsto ZX \in \mathbf{Mat}(m,k) $$
のことであり,次の図式で表されます。
![写像 !FORMULA[120][1748735021][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FohqrAl7RASpzKrhMfClm.png?alt=media) 写像 $\yoneda{X}{_k} = \Endash \c X$
写像 $\yoneda{X}{_k} = \Endash \c X$
ここでは圏$\mathbf{Mat}$の例を述べましたが,より一般の圏に対しても同様の議論が行なえます。
米田写像の自然性
米田写像$\alpha_{X,c}$が同型射であることをすでに述べました。米田の補題では,さらにこの同型が$X$と$c$について自然であることを主張しています。この自然性について説明するとやや煩雑になりますので,ここではこの自然性を明示的に表した次の命題を証明します。
米田写像$\alpha_{X,c} \colon \Func{\cC}{\Set}(\yoneda{c},X) \to Xc$は,任意の$\sigma \colon \Func{\cC}{\Set}(X,Y)$と任意の$p \in \cC(c,d)$($X,Y,c,d$も任意)について次式を満たす。
$$
(\sigma \b p) \c \alpha_{X,c} = \alpha_{Y,d} \c (\sigma \c \Endash \c \yoneda{p})
$$ $$\tag{1}\label{eq:nat}$$
式\eqref{eq:nat}は次の図式で表されます。
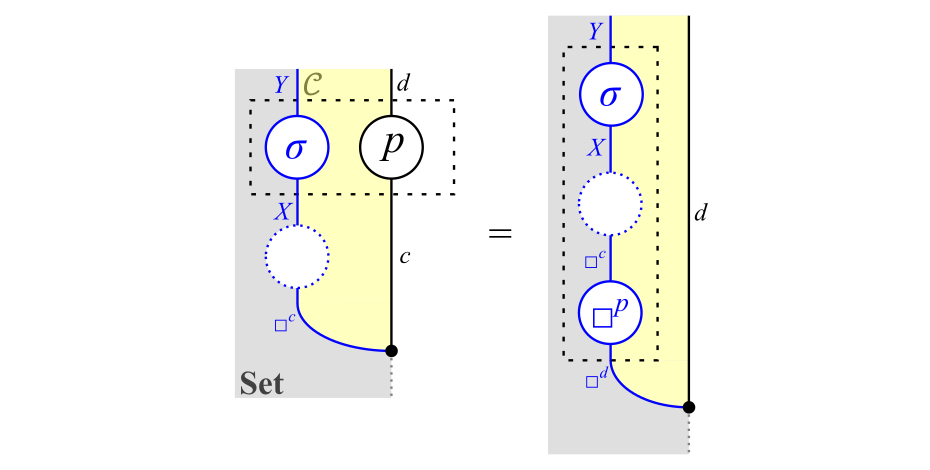 式\eqref{eq:nat}
$$\tag{2}\label{eq:nat_diagram}$$
式\eqref{eq:nat}
$$\tag{2}\label{eq:nat_diagram}$$
ただし,左辺および右辺の補助線で囲まれた箇所は,それぞれ写像$\sigma \b p \colon Xc \to Yd$および写像$\sigma \c \Endash \c \yoneda{p} \colon \Func{\cC}{\Set}(\yoneda{c},X) \to \Func{\cC}{\Set}(\yoneda{d},Y)$です。
$\yoneda{c}(p) = p \c \Endash$および$\yoneda{p}{}_d = \Endash \c p$より( 第10回の記事 を参照のこと),次式が成り立つ。
$$ \yoneda{c}(p)(1_c) = p \c 1_c = p = 1_d \c p = \yoneda{p}{}_d(1_d) $$
この最初と最後の式は次の図式で表される。
![式!FORMULA[137][783411527][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fl6NmLg5anLyTeUSz9oGA.png?alt=media) 式$\yoneda{c}(p)(1_c) = \yoneda{p}{}_d(1_d)$
式$\yoneda{c}(p)(1_c) = \yoneda{p}{}_d(1_d)$
この式を用いると,次のようにして式\eqref{eq:nat_diagram}を導ける。
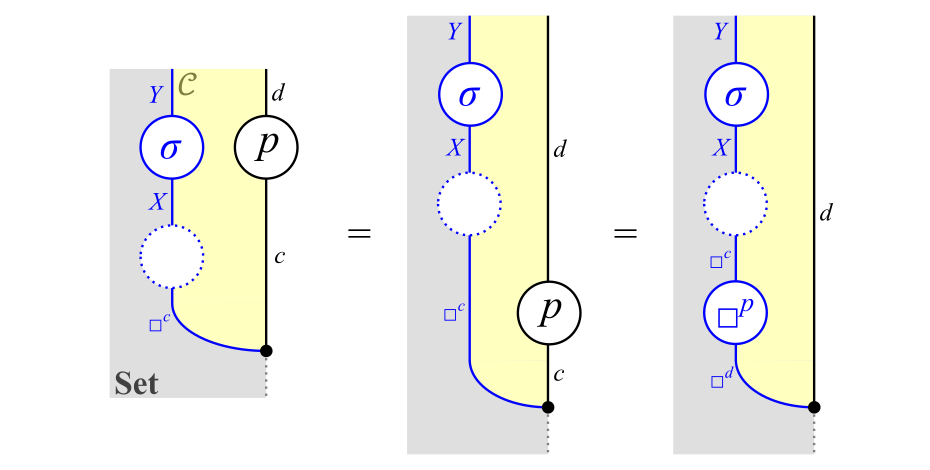 式\eqref{eq:nat_diagram}の証明
式\eqref{eq:nat_diagram}の証明
まとめ
「点線の枠による表記」を用いることで,米田の補題を視覚的にわかりやすい形で証明できることを述べました。米田の補題に限らず,ホムセットが登場する話題では「点線の枠による表記」を用いるとしばしば便利です。
