【ストリング図で学ぶ圏論 #11】ホム関手のストリング図（後編）

はじめに

この記事では， 前回の記事 で紹介した「点線の枠による表記」について，より詳しく説明します。

本連載の目次

#1： 圏の定義と具体例
#2： 関手と自然変換
#3： 垂直合成と水平合成
#4： モノイダル圏
#5： モナドとは自己関手の圏におけるモノイド対象のこと
#6： モナドの例
#7： 随伴
#8： 関手を表す線の順序の交換
#9： 普遍射と随伴・極限・カン拡張
#10： ホム関手のストリング図（前編）
#11： ホム関手のストリング図（後編）（この記事）
#12： 米田の補題

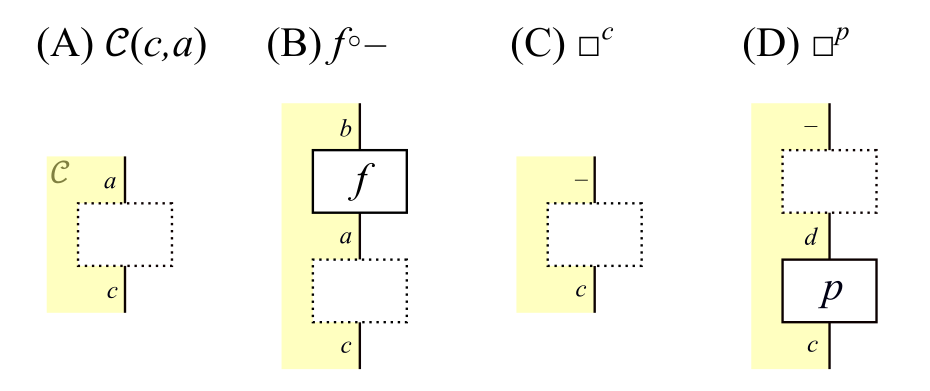
点線の枠による表記の規則

前回の記事 の「まとめ」では，点線の枠による表記として次のような図式を紹介しました。

まとめ

この表記の規則の概要をまとめておきます（拙著Nak-2025でていねいに説明しています）。

規則(4)を利用すると，関手$F$や自然変換$\alpha$を「点線の枠による表記」で素直に表せます。具体的には，$F$や$\alpha$を対象$a$に作用させた$F \b a = Fa$や$\alpha \b a = \alpha_a$の図式を描いて，その図式の線$a$を線「$\Endash$」に置き換えれば$F$や$\alpha$の図式が得られます。対象$a$に作用させる代わりに，射$f$に作用させた図式を考えても同様です。

これから示す具体例を考えれば，イメージがつかめると思います。

集合値関手$\cC(c,G\Endash)$

$\cC(c,G\Endash)$の定義

ホム関手$\yoneda{c} \colon \cC \to \Set$（ただし$c \in \cC$）と関手$G \colon \cD \to \cC$との水平合成$\yoneda{c} \b G \colon \cD \to \Set$を$\cC(c,G\Endash)$と書くことにします。この関手を明示的に表すと，次のようになります。

• [対象への作用] $\cD$の各対象$a$を$\Set$の対象（つまり集合）$\cC(c,Ga)$に写す。
• [射への作用] $\cD$の各射$f \colon a \to b$（$a,b \in \cD$は任意）を$\Set$の射（つまり写像）$(Gf \c \Endash)_c \colon \cC(c,Ga) \to \cC(c,Gb)$に写す。

$\cC(c,G\Endash)$の図式

関手$\cC(c,G\Endash)$は，次の図式で表されます。

関手$\cC(c,G\Endash)$
$$\tag{1}\label{eq:1}$$

この右辺が点線の枠による表記です。このように表せることは，この関手の対象への作用または射への作用を考えればわかります。実際，関手$\cC(c,G\Endash)$を対象$a \in \cC$に作用させると

$\cC(c,G\Endash) \b a$

となり，これらは$\cC(c,Ga)$を表しています。この右辺の図式における線$a$を線「$\Endash$」に置き換えることで式\eqref{eq:1}の右辺の図式が得られます。なお，関手$\cC(c,G\Endash)$を射$f \in \mor \cC$に作用させた

$\cC(c,G\Endash) \b f$
$$\tag{2}\label{eq:2}$$

を考え，この右辺の図式におけるブロック$f$を線「$\Endash$」に置き換えることでも得られます。

$\cC(c,G\Endash)$は2個の関手の水平合成ですので，明らかに関手であり，したがって合成を保ちます。$\cC(c,G\Endash)$が合成を保つことは，次の図式からも確認できます。

$\cC(c,G\Endash)$が合成を保つことの確認

2番目の式は，式\eqref{eq:2}の右辺の$f$に$gf$を代入したものです。3番目の式は，写像の合成$(Gg \c \Endash) \c (Gf \c \Endash)$を表しており，$(Gg \c \Endash)$を表す図式（つまり式\eqref{eq:2}の右辺の$f$に$g$を代入したもの）における点線の枠に$(Gf \c \Endash)$を表す図式（つまり補助線で囲まれた部分であり，これは式\eqref{eq:2}の右辺そのもの）を入れたものとして表しています。2番目と3番目の式は，補助線を削除すればまったく同じです。このように，関手$\cC(c,G\Endash)$を点線の枠による表記で表すと，合成を保つことが視覚的に明らかになります。

集合値関手$\cC(c,G\Endash)$から集合値関手$\cE(e,F\Endash)$への自然変換

具体例

集合値関手$\cC(c,G\Endash)$から集合値関手$\cE(e,F\Endash)$への自然変換について考えます（ただし，$G \colon \cD \to \cC$および$F \colon \cD \to \cE$）。やや複雑な具体例として，次のように定められる自然変換$\tau$を考えることにします。

自然変換$\tau$

ただし，関手$H$と射$f$と自然変換$\alpha$は任意です。$\tau$が自然変換であることは，後で確認します。この右側の図式は，射$\tau_x$の点線の枠による表記です。$\tau$の点線の枠による表記は，この図式の線$x$を線$\Endash$に置き換えたものとして

$\tau$の点線の枠による表記
$$\tag{3}\label{eq:3}$$

の右辺のようになります。

$\tau$が自然変換である，つまり$\tau$が自然性を満たすことを確認しておきます。$\tau$の自然性は，各射$g \in \cD(x,y)$（$x,y \in \cD$は任意）について

$\tau$の自然性

を満たすこととして表されます。この等号が成り立つことは，次式からわかります。

$\tau$の自然性（点線の枠による表記）
$\tag{4}\label{eq:4}$

実際，両辺から補助線を削除して，2個のブロック$\alpha$と$g$を線に沿って動かせば，左辺から右辺がすぐに得られます。

一般化した場合

集合値関手$\cC(c,G\Endash)$から集合値関手$\cE(e,F\Endash)$への任意の自然変換$\tau$を，次の図式で表すことにします。

$\cC(c,G\Endash)$から$\cE(e,F\Endash)$への任意の自然変換$\tau$
$\tag{5}\label{eq:5}$

とくに式\eqref{eq:3}の自然変換$\tau$は，この特別な場合とみなせます。

式\eqref{eq:3}の自然変換$\tau$

直観的には，この右辺の$\alpha,H,f$の部分をブラックボックスと捉えたものが左辺のブロック$\tau$であると考えると，わかりやすいかもしれません。式\eqref{eq:5}の自然変換$\tau$の自然性は，$\cD$ の各射$g$に対して

式\eqref{eq:5}の自然変換$\tau$の自然性

を満たすものとして表されます。この式は式\eqref{eq:4}を一般化したような形をしていることがわかると思います。このように表すと，「射$g$が自然変換$\tau$を素通りする」という直観的なイメージを素直な形で表せるため，便利です。このように，式\eqref{eq:3}のような表記には，その図式から$\tau$の自然性を直観的でわかりやすい形で表せるという利点があります。

まとめ

集合値関手$\cC(c,G\Endash)$と，集合値関手$\cC(c,G\Endash)$から集合値関手$\cE(e,F\Endash)$への自然変換の図式について述べました。点線の枠による表記を用いると，これらの関手や自然変換を直観的でわかりやすい形で表せることを示しました。