【ストリング図で学ぶ圏論 #2】関手と自然変換

はじめに

前回の記事 では，圏の定義といくつかの例を紹介しました。今回は，関手と自然変換について説明します。ストリング図を用いると，関手や自然変換を素直な形で表せます。

本連載の目次

#1： 圏の定義と具体例
#2： 関手と自然変換（この記事）
#3： 垂直合成と水平合成
#4： モノイダル圏
#5： モナドとは自己関手の圏におけるモノイド対象のこと
#6： モナドの例
#7： 随伴

関手

関手の定義

まず，関手の定義を示します。すぐ後で紹介する関手の図式を理解すると，イメージをつかみやすいと思います。

$\cC$から$\cD$への関手$F$を$F \colon \cC \to \cD$（または$F \in \cD^\cC$）と書きます。また，$\cC$から$\cC$への関手を$\cC$上の関手とよびます。

関手の図式

図式では，関手$F \colon \cC \to \cD$を次のような線で表すことにします。

関手$F$

対象$a \in \cC$を$F$で写して得られる対象$Fa$を次のように表します。

対象$Fa$ $$\tag{1}\label{eq:Fa}$$

この左辺は対象$a$を関手$F$で写した結果を表しており，右辺は対象$Fa$を表しています（関手の定義よりこれらは同じです）。直観的には，左辺のように並列に並んだ2本の線$F$と$a$を横方向に移動させて重ねると，右辺のように1本の線$Fa$になると解釈できます。$Fa$が$\cD$の対象であることは，右辺にある線$Fa$の左側の領域が$\cD$になっていることから読み取れます。

また，射$f \in \cC(a,b)$を$F$で写して得られる射$Ff$を次式のように表します。

射$Ff$ $$\tag{2}\label{eq:Ff}$$

対象の場合と同様に，左辺は対象$f$を関手$F$で写した結果を表しており，右辺は射$Ff$を表しています（やはり，これらは同じです）。直観的には，左辺のように並列に並んだ線$F$とブロック$f$を横方向に移動させて重ねると右辺のようにブロック$Ff$になると解釈できます。この際，

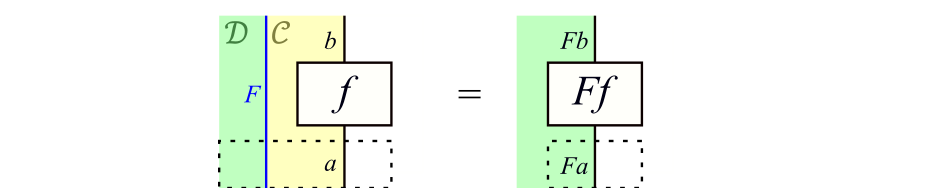式\eqref{eq:Ff}に補助線を描いたもの

の補助線で囲まれた箇所のように，ブロック$f$の下側にある線$a$は線$F$と重なって1本の線$Fa$になると解釈できます。線$b$についても同様です。

これらの図式が表しているように，対象や射と関手との合成は「横方向の合成」とみなせます。このことは，射の合成が「縦方向の合成」とみなせたことと対照的です。

上で導入した図式を用いて，条件(F1)～(F3)がどのように表されるかを説明します。

条件(F1)

条件(F1)では，関手$F$により$f$のドメイン$a$が$Fa$に写り，$f$のコドメイン$b$が$Fb$に写ることを主張しています。図式では

再掲：式\eqref{eq:Ff}に補助線を描いたもの

の補助線で囲まれた箇所が$a$を$Fa$に写すことを主張しています。$b$を$Fb$に写すことも同様です。

条件(F2)

条件(F2)の合成の保存$F(gf) = (Fg)(Ff)$は，次式にように表せます。

条件(F2)：合成の保存

ここで，補助線は「先に演算する」ことを表していると思ってください。左辺が$F(gf)$を表しており，右辺が$(Fg)(Ff)$を表しています。条件(F2)より左辺と右辺は等しいため，この図式から補助線を削除しても問題ありません。

条件(F3)

条件(F3)の恒等射の保存は，「$\cC$の各恒等射$1_a$を$\cD$の恒等射$1_{Fa}$に写す」と言い換えられます（条件(F1)より，$F1_a$のドメインとコドメインは$Fa$でなければならないためです）。この条件は，式\eqref{eq:Fa}の図式

対象$Fa$（を恒等射$1_Fa$とみなしたもの） $$\tag{1}$$

において線$a$および線$Fa$をそれぞれ恒等射$1_a$および$1_{Fa}$のことだとみなしても問題ないことを意味しています。実際，図式では各対象$a$と恒等射$1_a$を区別できないため，もしこの条件が成り立たなければ式\eqref{eq:Fa}のように表すと都合が悪いことがわかるでしょう。このように，式\eqref{eq:Fa}のように表しても不都合が生じないことを保証しているのが条件(F3)であるといえます。

条件(F3)は，次の図式で表すこともできます。

条件(F3)の恒等射の保存（式\eqref{eq:Fa}の別表記）

左辺および右辺における補助線で囲まれた箇所は，どちらも恒等射を表しています（それぞれ$1_a$および$1_{Fa}$です）。この等号が成り立ちますので，この図式から補助線を削除しても問題ありません。

これまでに述べたことを図式の観点で大雑把に捉えると，関手$F$の定義とは，線$F$を上の図式のように表したときに$F$が満たしていると望ましいと思われる条件を与えたものにほかならないといえそうです。

関手は射への作用のみから一意に定まる

関手$F \colon \cC \to \cD$が与えられたとき，$F$はその射への作用のみから一意に定まります。このことは，$\cC$の各対象が恒等射と同一視できることと条件(F1)から容易にわかると思います。

関手の例

関手の例をいくつか挙げます。これらの例のうち，わからないものがあれば無視しても構いません（後で述べる自然変換の例も同様です）。

写像

前回の記事 で述べたように，任意の集合$X$は離散圏（つまり恒等射のみをもつ圏）とみなせます。$X$の各要素$x$が対象$x$（および恒等射$1_x$）と同一視されるのでした。このようにみなしたとき，以下が成り立ちます。

モノイド準同型

前回の記事 では，1個の対象から成る圏$\cM$をモノイドとよび，$\cM$の射の集合$\bM$もモノイドとよびました（$\cM$と$\bM$は実質的に同一視できるのでした）。

モノイド$\bM$からモノイド$\bM'$へのモノイド準同型とよばれる写像を定義しておきます。

以下が成り立ちます。

恒等関手

対象への作用と射への作用がともに恒等写像であるような$\cC$上の関手を，恒等関手とよび$1_\cC$と書きます。この関手は，$\cC$の各対象$c$を$c$自身に写し，$\cC$の各射$f$を$f$自身に写します。

ベクトル空間の基底の変換

各ベクトル空間$\V$に対して$\V$上の可逆な線形写像$\phi_\V$を一つずつ選んだとき，次のような関手$\Phi \colon \VecK \to \VecK$が考えられます。

• $\VecK$の各対象（つまりベクトル空間）$\V$を$\V$自身に写す。
• $\VecK$の各射（つまり線形写像）$f \colon \V \to \W$を射（つまり線形写像）$\phi_\W \c f \c \phi_\V^{-1} \colon \V \to \W$に写す。

$\Phi f = \phi_\W \c f \c \phi_\V^{-1}$は，次の図式で表されます。

$\Phi f = \phi_\W \c f \c \phi_\V^{-1}$

ある観点では，この関手は各$\V$について$\V$の基底$\{ v_i \}_i$を基底$\{ \phi_\V(v_i) \}_i$に変えるような働きをすると解釈できます。

任意の対象は関手とみなせる

1個の対象（$*$とおきます）のみをもつ離散圏を$\cOne$と書きます。この圏$\cOne$の射は$1_*$のみですので，$\cOne$から任意の圏$\cC$への任意の関手$F$は$F 1_* = 1_{F*}$のみにより定まります。このため，関手$F \colon \cOne \to \cC$は$\cC$の対象$c \coloneqq F*$と同一視できます。逆に，任意に選んだ$\cC$の対象$c$に対して，写像$\mor \cOne \ni 1_* \mapsto 1_c \in \mor \cC$を射への作用とするような関手$F \colon \cOne \to \cC$が一意に定まります。このようにして，任意の圏$\cC$の任意の対象$c$は$\cOne$から$\cC$への関手$F$と同一視できます。この連載では，しばしば対象を関手とみなします。

自然変換

自然変換の定義

自然変換の定義を示します。関手の場合と同様に，すぐ後で紹介する自然変換の図式を理解するとイメージしやすいと思います。

ここで，集まり$\alpha \coloneqq \{ \alpha_a \}_{a \in \cC}$が$a$で添字付けられているとは，単なる（$a$で添字付けられていない）集まりとは異なり，各$a \in \cC$に対応する$\alpha$の要素$\alpha_a$が定まっているという意味です。この添字付けられた集まり$\alpha$は，$\cC$の各対象$a$を$\cD$のある射$\alpha_a$に写すような写像と言い換えることもできます。この写像は，$\alpha$の対象への作用とよばれます。以降では，添字付けられた集まりのことも単に集まりとよぶ場合がしばしばあります。なお，定義では$\alpha_a$が$\cD(Fa,Ga)$の要素（つまり$\cD$の$Fa$から$Ga$への射）であることも主張しています。

このような自然変換を，$\alpha \colon F \nto G$（または$\alpha \in \cD^\cC(F,G)$）と書きます。また，各$\alpha_a$を$\alpha$の成分とよびます。

自然変換の図式

自然変換$\alpha \colon F \nto G$を次のブロックで表すことにします。

自然変換$\alpha$

また，$\alpha$の各成分$\alpha_a$（つまり対象$a$に対応する射）を次のように表します。

自然変換$\alpha$の成分$\alpha_a$ $$\tag{3}\label{eq:alpha_a}$$

この右辺は射$\alpha_a \colon Fa \to Ga$を表しています。（なお，ブロック$\alpha_a$の下側からは2本の線$F$と$a$が伸びており，これらは式\eqref{eq:Fa}で述べたように対象$Fa$を表しています。同様に，ブロック$\alpha_a$の上側にある2本の線$G$と$a$は対象$Ga$を表しています。）左辺では，ブロック$\alpha$を線$a$の左側に並べることでこの射$\alpha_a$を表しています。$\alpha$の対象への作用を考えると，$\alpha_a$は$a$を$\alpha$で写したものとみなせます。式\eqref{eq:alpha_a}は，ブロック$\alpha$と線$a$を横方向に移動させて重ねるとブロック$\alpha_a$になると解釈できます。

自然性

条件(N)の自然性は次のように表されます。

$\alpha$の自然性：$Gf \circ \alpha_a = \alpha_b \circ Ff$ $$\tag{4}\label{eq:alpha_f}$$

ただし，補助線で囲まれた部分を先に演算するものとします。直観的には，この等式は「射$f$と自然変換$\alpha$をそれぞれ線に沿って動かすことで，それらの縦方向の位置を自由に変えることができる」とみなせます。このように，自然変換$\alpha$をブロックで表せば，その自然性を表す式\eqref{eq:alpha_f}を視覚的にわかりやすい形で表せます。

この式は，式\eqref{eq:alpha_a}の右辺の表記を用いると，次のようにも表されます。

$\alpha$の自然性 $$\tag{5}\label{eq:alpha_nat}$$

式\eqref{eq:alpha_f}や式\eqref{eq:alpha_nat}は，「射$f$が自然変換$\alpha$を素通りできる」のように解釈してもよいと思います。実際，式\eqref{eq:alpha_nat}は，「左辺のブロック$f$が$\alpha_a$を素通りして$\alpha_a$の下側に移動できて，この移動により右辺のようになる」のように解釈できます。

任意の（$a \in \cC$で添字付けられた）射の集まり$\alpha = \{ \alpha_a \colon Fa \to Ga \}_{a \in \cC}$が自然変換であるとは限りません。$\alpha$が自然変換ではない（つまり自然性を満たさない）場合には，$\alpha$を式\eqref{eq:alpha_a}の左辺のようなブロックとして表すことはできません。このため，射の集まり$\alpha$が与えられたとき，少なくとも$\alpha$が自然変換であることを確認できるまでは式\eqref{eq:alpha_nat}の左辺や右辺のような表記を用いるとよいと思います。

自然変換$\alpha$に対して，写像

$$ \mor \cC \ni f \mapsto \alpha \b f \coloneqq Gf \c \alpha_a \in \mor \cD $$

を$\alpha$の射への作用とよびます。射$\alpha \b f$（つまり，射$f$を$\alpha$で写したもの）は次の図式で表されます。

射$\alpha \b f$

ただし，等号では式\eqref{eq:alpha_f}を用いています。

同型射と自然同型

ここで，今後のために同型射と自然同型について述べておきます。$\cD$の射$f$についてある射$g$が存在して$gf$と$fg$が恒等射であるとき，$f$を同型射とよびます。また，$g$を$f$の逆射とよび$f^{-1}$と書きます。$f$が同型射ならば$f^{-1}$は一意に定まります（証明は割愛します）。

自然変換$\alpha$の各成分$\alpha_a$が同型射であるとき，$\alpha$を自然同型とよびます。関手$F$から関手$G$への任意の自然同型$\alpha = \{ \alpha_a \}_{a \in \cC}$に対して，その各成分の逆射の集まり$\alpha^{-1} \coloneqq \{ \alpha_a^{-1} \}_{a \in \cC}$は$G$から$F$への自然同型です（証明は割愛します）。

自然変換の例

恒等自然変換

任意の関手$F \colon \cC \to \cD$に対し，$1_F$$\coloneqq \{ 1_{Fa} \}_{a \in \cC}$は$F$から$F$への自然変換です。実際，$1_F$の自然性を表す式は$Ff \circ 1_{Fa} = 1_{Fb} \circ Ff$であり，これが成り立つことは両辺がともに$Ff$に等しいことから明らかです。$1_F$を$F$上の恒等自然変換とよびます。

任意の射は自然変換とみなせる

任意の圏$\cC$の任意の射$f \in \cC(a,b)$（$a,b \in \cC$も任意）について考えます。関手の例で述べたように，対象$a,b \in \cC$は$\cOne$から$\cC$への関手とみなせます。同様に，射$f$は関手$a$から関手$b$への自然変換とみなせます。厳密に書くと，$\{ f \}_{* \in \cOne}$は関手$a \colon \cOne \to \cC$から関手$b \colon \cOne \to \cC$への自然変換です（自然性を満たすことは，$\cOne$の射が恒等射$1_*$のみであることからすぐにわかります）。$\cOne$の対象は$*$のみですので，$f$と$\{ f \}_{* \in \cOne}$を同一視できます。この連載では，しばしばこれらを同一視して任意の射$f$を自然変換とみなします。

ベクトルの和

ベクトル空間$\V$の要素の和（$+_\V$とおく）は，直和空間$\V \oplus \V$から$\V$への線形写像として

$$ +_\V \colon \V \oplus \V \ni \braket{v,w} \mapsto v + w \in \V $$

のように表せます。また，直和$\oplus$は以下により定まる$\VecK$ 上の関手とみなせます。

• $\VecK$の各対象（つまりベクトル空間）$\V$を$\V \oplus \V$に写す。
• $\VecK$の各射（つまり線形写像）$f$を$f \oplus f$に写す。

このとき，「各$\V \in \VecK$の和の集まり」$+ \coloneqq \{ +_\V \}_{\V \in \VecK}$は，直和$\oplus$から恒等関手$1_{\VecK}$への自然変換です。直観的には，この集まりが自然変換であることは，「各ベクトル空間$\V$における和$+_\V$という演算が，ベクトル空間毎に互いに無関係に定められているのではなく，ある種の整合性を保っている」と解釈できそうです。また，この「ある種の整合性」を定式化したものが先述の自然性であるといえます。

$+$が自然変換であることを確認しておきましょう。このことは，

$+$の自然性 $$\tag{6}\label{eq:Vec_plus}$$

を満たすことからわかります。実際，（$\VecK$における射の合成は写像の合成ですので）この左辺は写像の合成$f \c +_\V$を表しており，この写像は各$\braket{v,w} \in \V \oplus \V$を$f(v + w) \in \W$に写します。また，右辺は写像の合成$+_\W \c(\oplus f)$を表しており，この写像は各$\braket{v,w} \in \V \oplus \V$を$f(v) + f(w) \in \W$に写します。$\VecK$の射$f$は線形写像ですので$f(v + w) = f(v) + f(w)$が成り立ち，したがってこれらの写像が等しいことがわかります。

なお，$\braket{v,w} \in \V \oplus \V$に式\eqref{eq:Vec_plus}の両辺で表される写像を施した結果，つまり

$$ (f \c +_\V) \braket{v,w} = (+_\W \c(\oplus f)) \braket{v,w} $$

は，次の図式で表せます。

$(f \c +_\V) \braket{v,w} = (+_\W \c(\oplus f)) \braket{v,w}$を表す図式

前回の記事 では集合$X$の要素$x$を写像$\{*\} \ni * \mapsto x \in X$と同一視できることを述べましたが，ベクトル空間の要素に対してもこれと同様の同一視が行えます。具体的には，任意のベクトル空間$\V$の任意の要素$v$は線形写像$\tilde{v} \colon \K \ni k \mapsto k \cdot v \in \V$と同一視できます。この図式では，$\V \oplus \V$の要素$\braket{v,w}$に対してこのような同一視を行って，$\braket{v,w}$を$\K$から$\V \oplus \V$への射（つまり線形写像）として表しています。

このように表すと，この図式の左辺は「$\braket{v,w}$に写像$+_\V$を施してから写像$f$を施したもの」と読めます（図式の下側から上側に向かって読むとわかりやすいかと思います）。同様に，右辺は「$\braket{v,w}$に写像$\oplus f$（つまり$f \oplus f$）を施してから写像$+_\W$を施したもの」と読めます。この図式が各$\braket{v,w} \in \V \oplus \V$に対して成り立ちますので，式\eqref{eq:Vec_plus}が成り立つことがわかります。

自然変換$+$をブロックで表すと，式\eqref{eq:Vec_plus}は次のようにも表せます。

$+$の自然性（別表現）

ただし，恒等関手を表す線（つまり，ブロック$+$の上側から伸びているはずの線）は，この図式のようにしばしば省略します。

ベクトルの定数倍

和と同様に，「各ベクトルを$k$倍する」という演算も自然変換とみなせます。具体的には，各$\V \in \VecK$と各$k \in \K$について，$\V$上の射（つまり線形写像）$\V \ni v \mapsto kv \in \V$を$(\times k)_\V$とおきます。このとき，「各$\V \in \VecK$の$k$倍の集まり」$\times k \coloneqq \{ (\times k)_\V \}_{\V \in \VecK}$は恒等関手$1_{\VecK}$から恒等関手$1_{\VecK}$への自然変換です。$\times k$の自然性は，次式のように表せます。

$\times k$の自然性

実際，この左辺および右辺は各$v \in \V$をそれぞれ$f(kv) \in \W$および$k \cdot f(v) \in \W$に写す写像であり，$f$は線形写像ですので等号が成り立ちます。

可換モノイドの積

可換モノイドの積$\c$についても上記の「ベクトルの和$+$」と同じ議論ができます。具体的には，「各$\cM \in \CMon$における積（$\c_\cM$とおきます）の集まり」$\c \coloneqq \{ \c_\cM \}_{\cM \in \CMon}$は，関手$\times$（後述）から恒等関手$1_{\CMon}$への自然変換です。なお，可換モノイドの圏$\CMon$については， 前回の記事 を参照してください。

$\c$の自然性は，次式により表されます。

$\c$の自然性

ここで，関手$\times$は以下により定まる$\CMon$上の関手です。

• $\CMon$の各対象（つまり可換モノイド）$\cM$を$\cM \times \cM$に写す。
• $\CMon$の各射（つまりモノイド準同型）$f$を$\braket{f,f}$（$f$と$f$の組のこと）に写す。

また，各$\cM \in \CMon$に対して直積$\cM \times \cM$から$\cM$への写像$\c_\cM$を

$$ \c_\cM \colon \cM \times \cM \ni \braket{x,y} \mapsto x \c y \in \cM $$ $$\tag{7}\label{eq:CMonC}$$

と定めます（モノイド準同型になります）。この写像は，$\cM$における積を表しています。このとき，$\c \coloneqq \{ \c_\cM \}_{\cM \in \CMon}$が自然変換であることを容易に確認できます（ただし，ここでは割愛します）。

ベクトル空間の基底の変換

関手の例で紹介した「ベクトル空間の基底の変換」を表す関手$\Phi \colon \VecK \to \VecK$を考えます。この関手では，各ベクトル空間$\V$に対して$\V$上の可逆な線形写像$\phi_\V$を一つずつ選んだのでした。このとき，これらの線形写像の集まり$\phi \coloneqq \{ \phi_\V \}_{\V \in \VecK}$は$1_{\VecK}$から$\Phi$への自然同型であり，$\phi^{-1} = \{ \phi_\V^{-1} \}_{\V \in \VecK}$は$\Phi$から$1_{\VecK}$への自然同型です。

$\phi$の自然性は次式で表せます。

$\phi$の自然性

実際，この左辺は写像の合成$(\Phi f) \c \phi_\V$であり，この写像は各$v \in \V$を$(\phi_\W \c f \c \phi^{-1}_\V) \c \phi_\V(v) = \phi_\W(f(v))$に写します。一方，右辺は写像の合成$\phi_\W \c f$であり，この写像は各$v \in \V$を$\phi_\W(f(v))$に写します。このため，等号が成り立ちます。

なお，各ベクトル空間$\V$について$\phi_\V^{-1} \c \phi_\V = 1_\V$が成り立ちますが，この式は次の図式で表せます。

$\phi^{-1}$と$\phi$の合成

まとめ

関手と自然変換の定義を述べ，これらを図式で表す方法を紹介しました。関手を線で表して自然変換をブロックで表すことで，それらが満たすべき規則をわかりやすい形で表せることを説明しました。

次回以降の記事では，このような図式を用いて関手や自然変換の合成について述べる予定です。