文献あり

【ストリング図で学ぶ圏論 #1】圏の定義と具体例

3767

はじめに

ストリング図は，圏論のいくつかの概念を視覚的にわかりやすい形で表すための強力なツールとして知られています。圏論の基礎的な書籍では，ストリング図よりも可換図式が用いられていることが多いと思いますが，個人的には圏論の基礎を学ぶ際にもストリング図を用いたほうがわかりやすい場面が少なくないのではないかと考えています（人によるとは思いますが）。

そこで，ストリング図の威力とおもしろさを伝えられたらと思い，連載記事を書くことにしました。この連載では，圏論の初学者を主な対象とし，数学を専門としない人でもある程度理解しやすいように書きたいと思います。

初回である今回の記事では，圏の定義を説明しつつ，ストリング図を紹介します。また，圏の具体例をいくつか挙げます。なお，今回の記事ではストリング図が活躍する場面はあまりありませんが，今後の記事ではストリング図が威力を発揮する場面が増えると思います。

補足：

この連載では，拙著『ストリング図で学ぶ圏論の基礎』 Nak-2025の一部を紹介します。各概念についての詳しい説明は，本書をご参照ください。

本連載の目次

#1：圏の定義と具体例（この記事）
#2：関手と自然変換
#3：垂直合成と水平合成
#4：モノイダル圏
#5：モナドとは自己関手の圏におけるモノイド対象のこと
#6：モナドの例
#7：随伴
#8：関手を表す線の順序の交換
#9：普遍射と随伴・極限・カン拡張
#10：ホム関手のストリング図（前編）
#11：ホム関手のストリング図（後編）
#12：米田の補題
番外編1：視覚的に理解するクライスリトリプルとモナドの同値性

圏の定義

まず，圏の定義を示します。圏になじみがない読者にとってはこの定義は難しいと感じるかもしれません。しかし，この定義をすぐに完全に理解できなくても構いません。すぐ後で行う補足説明やその後で示す圏の具体例を読めば，理解が深まるのではないかと思います。

圏

圏$\cC$とは「対象とよばれるもの」の集まりと「射とよばれるもの」の集まりから構成され，次の条件をすべて満たすものである。

各射はドメインとよばれる対象とコドメインとよばれる対象を一つずつもつ。以降では，ドメインが$a$でありコドメインが$b$である射$f$を$a$から$b$への射とよび，$f \colon a \to b$と書く。
2本の任意の射$f \colon a \to b, ~g \colon b \to c$（対象$a,b,c$も任意）について，$f$と$g$の合成とよばれる射$gf$（$g \c f$と書くこともある）が一意に定まって$gf \colon a \to c$である。
結合律：3本の任意の射$f \colon a \to b,~g \colon b \to c,~h \colon c \to d$（対象$a,b,c,d$も任意）について，$h(gf) = (hg)f$が成り立つ。
単位律：各対象$a$に対して$a$の恒等射とよばれる射$1_a \colon a \to a$が存在し，任意の射$f \colon a \to b$（対象$a,b$も任意）に対して$1_b f = f = f 1_a$を満たす。

規則1：射のドメインとコドメイン

以降では，ストリング図のことをしばしば単に図式とよぶことにします。

各射$f$を次の図式で表すことにします。

射!FORMULA[24][37794][0] 射$f$ $$\tag{1}\label{eq:f}$$

規則1は，射をこの図式のように表せることを主張していると考えるとわかりやすいかもしれません。

四角形のブロック$f$が$\cC$の射を表しており，その上下から伸びた2本の線$a,b$が$\cC$の対象を表しています。これらが圏$\cC$の射や対象であることを表すため，ブロックや線の左側の領域に色（ここでは黄色）を付け，さらにラベル「$\cC$」を付けています。なお，$f$を表すブロックの形は四角である必要はなく，丸などでも構いません。

ブロック$f$の上下からは線が1本ずつ伸びています。下側から伸びた線が$f$のドメイン$a$を表しており，上側から伸びた線が$f$のコドメイン$b$を表しています。規則1により各射$f$はドメイン$a$とコドメイン$b$を一つずつもつため，各射$f$に対して$a$と$b$が定まっています。

以降では，$\cC$の対象の集まりを$\ob \cC$と書き（$\ob$はobjectの意味），$\cC$の射の集まりを$\mor \cC$と書きます（$\mor$はmorphismの意味）。また，圏$\cC$の$a$から$b$への射全体の集まりを$\cC(a,b)$と書きます。射$f$のドメインを$\dom f$と書き，コドメインを$\cod f$と書きます。$a$が$\cC$の対象であることは$a \in \ob \cC$と表せますが，この代わりに$a \in \cC$と書くことがしばしばあります。$a$から$a$自身への射を，しばしば$a$上の射とよびます。

補足：

式\eqref{eq:f}には，「射$f$が圏$\cC$に属しており，ドメインが$a$でコドメインが$b$」という情報が含まれています。数式でも$f \in \cC(a,b)$のように表せば，これらの情報をすべて含められます。

規則2：射の合成

規則2は，2本の射$f$と$g$を任意に選んだとき，$f$のコドメイン（つまりブロック$f$の上側の線）と$g$のドメイン（つまりブロック$g$の下側の線）が等しいならば合成できるという規則です。図式では，合成は次に示すように「縦方向につなげる」ことで表されます。

射の合成!FORMULA[75][1174657][0] 射の合成$gf$

この式の左辺は2本の射$f$と$g$の合成を表しており，右辺は合成後の射$gf$を表していると解釈すると，わかりやすいかもしれません。この右辺が示すように，合成後の射$gf$のドメインは$a$であり，コドメインは$c$です。以降では，射$gf$のように述べた場合には，しばしば断りなく$f$と$g$が合成可能である（つまり$f$のコドメインと$g$のドメインが等しい）ことを仮定しているとします。

なお，この図式の右辺における黄色の領域では，ラベル$\cC$を省略しています。この図式のように，同じ圏は同じ色で表すものとし，重複するラベルは通常は省略します。

規則3：結合律

規則3では，結合律とよばれる条件について述べられています。結合律$h(gf)=(hg)f$は，次の図式で表されます。

結合律：!FORMULA[89][-751046441][0] 結合律：$h(gf)=(hg)f$

この図式の破線は補助線を表しており，ここでは補助線内の合成を先に行うことを意味するものと思ってください。このため，左辺は$h(gf)$，右辺は$(hg)f$を表しています。

この規則により$h(gf) = (hg)f$が成り立つことが保証されていますので，$h(gf)$や$(hg)f$のことを$hgf$と書いても厳密性が損なわれることはありません。上のような図式においては，両辺から補助線を削除しても問題ないことを意味します。このため，しばしば$hgf$のように書いたり，上のような図式から補助線を削除したりすることにします。

補足：

結合律を満たす限り，4本以上の射についても同様に合成の順序に依存しないことを示せます。たとえば$(i(hg))f = (ih)(gf)$が成り立ちます。

規則4：単位律

規則4では，単位律とよばれる規則について述べられています。以降では，対象$a$の恒等射$1_a \colon a \to a$を次の図式で表すことにします。

恒等射!FORMULA[100][34800853][0] 恒等射$1_a$

このとき，単位律$1_b f = f = f 1_a$は次の図式で表されます。

単位律：!FORMULA[102][1006798869][0] 単位律：$1_b f = f = f 1_a$

左側の等号は，$f$に$1_b$を合成したものが$f$に等しいことを表しています。同様に，右側の等号は，$f$に$1_a$を合成したものが$f$に等しいことを表しています。このため，直観的には，恒等射との合成は「何もしないこと」と同じであると解釈できます。上の図式においては，恒等射を表す破線を（単なる補助線とみなして）省略しても問題ないといえます。中央の式と比べて，左辺では線$b$が長くなっており，右辺では線$a$が長くなっていますが，線の長さの違いは無視できると解釈できます。

また，上の図式は，恒等射$1_a$を「対象$a$と本質的に同じようなもの」と捉えても問題ないことを暗示しています。実際，図式では，$1_a$と$a$をどちらも単なる線で表して普段はこれらを区別しません。各対象$a$を恒等射$1_a$のことだとみなすと，圏とは（射の合成が結合律と単位律を満たすような）射の集まりのことであるといえます。

補足：

圏論の標準的な書籍などでは射と対象を区別して扱っています。しかし，各対象$a$を恒等射$1_a$に置き換えて圏の定義を書き直せることが知られており（たとえば文献Mac-2012の第I章），そのような定義を考えることで厳密性を損なわずに対象と恒等射を同一視できます。ただし，圏論に慣れていないうちはこのような同一視を行うと混乱を招く場面があると思いますので，この記事では対象と恒等射を区別することにします。

高度な話題：

圏論では，「小さい集合」とよばれる概念がしばしば登場します。この連載では，「小さい集合」とよばれる概念を「集合」とよび，集合を含む広い概念として，「小さい集合」とはよべないようなものも含めたものを「集まり」とよぶことにします。厳密には「集合」と「集まり」を区別する必要があるのですが，これらの違いを気にしない読者は「集まり」を「集合」と読み替えても構いません。なお，一般には任意に選んだ圏$\cC$について，集まり$\cC(a,b)$は「集合」とは限りません。この連載ではとくに断りなく各$a,b \in \cC$について$\cC(a,b)$は「集合」であると仮定します。この仮定が成り立つような圏$\cC$は，局所小圏とよばれます。

圏の具体例

圏の具体例は数多くありますが，ここではその一部のみを紹介します。これから示す例のうちわからないものがあれば無視しても構いません。

例1：対象が1個のみの場合（モノイド）

まず，対象が1個（$*$とおきます）のみであるような圏について考えます。このような圏はモノイドとよばれます。モノイド$\cM$は，その対象は$*$しかありませんから，射の集まり（$\bM$と表すことにします）のみから構成されているとみなせます。対象が$*$のみであることを考慮すると，モノイドの定義は次のように言い換えられます。

モノイド

集合$\bM$が次の規則をすべて満たすとき，モノイドとよぶ。
（備考：規則(1)～(3)が定義1の規則(2)～(4)にそれぞれ対応している。）

任意の$f,g \in \bM$に対して，$gf \in \bM$（積とよばれる）が一意に定まる。
結合律：任意の$f,g,h \in \bM$に対して$h(gf) = (hg)f$が成り立つ。
単位律：ある$1 \in \bM$が存在し（単位元とよばれる），任意の$f \in \bM$に対して$1 f = f = f 1$を満たす。

補足1：

通常，定義2を満たす集合$\bM$のことをモノイドとよびますが，ここでは1個の対象のみからなる圏$\cM$も（広義の意味で）モノイドとよんでいます。

補足2：

モノイドになじみのある方は，モノイドを（複数の対象をもつことができるように）一般化したものが圏であるという観点で捉えるとわかりやすいかもしれません。圏は，モノイドの多対象版とよばれることもあります。

なお，定義2における積は射の合成のことであり，単位元$1$は$*$の恒等射です。

モノイドの具体例をいくつか示します。

例1.1：自然数と和

0以上の整数を自然数とよび，自然数全体から成る集合を$\Natural$とおきます。$\bM=\Natural$であるような（つまり$\Natural$の各要素を射とするような）モノイドが考えられます。ただし，射$f,g \in \bM$の合成は自然数の和$f+g$とします。0が単位元です。

念のため，この例が規則2～4を満たすことを確認しておきます。規則2（射の合成）を満たすことは，たとえば次式からわかります。

射の合成の例（!FORMULA[146][1115354][0]と!FORMULA[147][1115385][0]の合成は!FORMULA[148][1115416][0]）射の合成の例（$+1$と$+2$の合成は$+3$）

ただし，わかりやすく表現するため，射（つまり自然数）$f$を表すブロックを「$+f$」のように表しています。より一般的には，任意の$f,g \in \bM$に対して$f+g \in \bM$が成り立ちます。なお，図式における線のラベル*は省略しています（モノイドは1個の対象しかもちませんので，線のラベルを省略しても問題ありません）。

規則3の結合律$h+(g+f) = (h + g) + f$を満たすことは，たとえば次式（を一般化したもの）から容易にわかります。

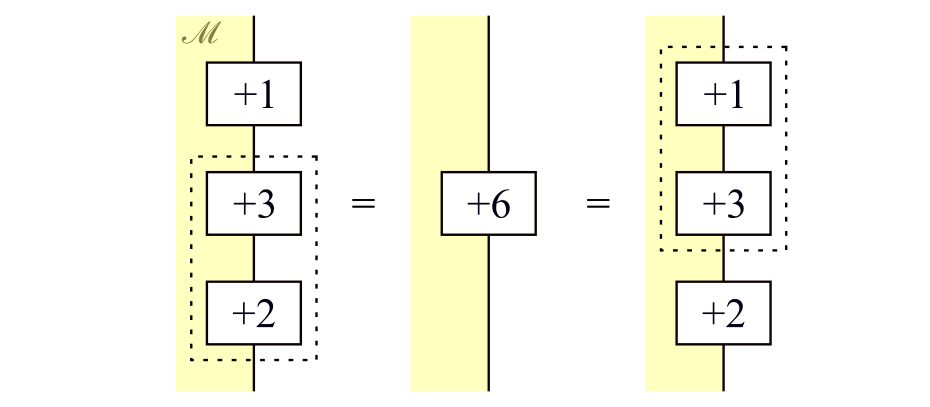結合律の例

規則4の単位律$0+f = f = f+0$を満たすことは，たとえば次式（を一般化したもの）からわかります。

単位律の例

以降の例では規則2～4を満たすことの確認は省略しますが，いずれの例でもすぐに確かめられると思います。

例1.2：群

群とよばれる構造は，モノイドの特別な場合です。具体的には，モノイドのうち，各射$f$に対して$f f^{-1} = 1 = f^{-1} f$（ただし$1$は単位元）を満たすような射$f^{-1}$（逆元とよばれます）が存在するようなものが群とよばれます。

補足：

群になじみのある方は
$$ \text{群} \quad\xrightarrow{\text{一般化}}\quad \text{モノイド} \quad\xrightarrow{\text{一般化}}\quad \text{圏} $$
のようなイメージで捉えると理解しやすいかもしれません。

例1.3：正方行列と積

1以上の整数$n$を固定したとき，$n$次正方行列を射とする，つまり$\bM$が$n$次正方行列全体であるようなモノイドが考えられます。射（つまり$n$次正方行列）$A,B \in \bM$の合成は行列としての積$BA$とします。$n$次単位行列が単位元です。なお，逆行列をもたないような$n$次正方行列が存在するため，このモノイドは群ではありません。

補足：

この連載では，行列を扱う場合が何度かありますが，行列の各成分は実数であるものとします。

例1.4：タスク

タスクを射とするモノイドが考えられます。ここで，タスクとは「朝食を食べる」や「歯を磨く」のような作業のことを表していると考えてください。射$f,g \in \bM$の合成$gf$は，タスク$f$を行った後でタスク$g$を行うという一連のタスクであるとします。たとえば，タスク「ドアの鍵をかける」とタスク「駅に出かける」の合成は，タスク「ドアの鍵をかけてから駅に出かける」です。「何もしない」が単位元です。（ただし，「何もしない」と任意のタスク$f$の合成はタスク$f$であり，タスク$f$と「何もしない」の合成もタスク$f$であるとします。）

補足：

例1.1における整数$f$を「$f$を足す」というタスクだと考えると，例1.1はこの例の特別な場合とみなせます。実際，$g+f$は「$f$を足してから$g$を足す」というタスクだといえます。同様に，例1.3における$n$次正方行列$A$を「任意の$n$次元ベクトル$x$を$n$次元ベクトル$Ax$に写す」というタスクだと考えると，例1.3はこの例の特別な場合とみなせます。

例2：対象が一般に複数ある場合

次に，モノイドとは限らない（つまり対象が一般に複数個ある）ような圏の例を挙げます。

例2.1：離散圏

極端な例として，恒等射以外の射をもたない圏を考えます。このような圏は，離散圏とよばれます。離散圏では射は恒等射しかありませんので，対象の集まりが定まれば射の集まりは自動的に定まります。とくに，任意の集合$X$は，$X$の各要素$x$を対象$x$（および恒等射$1_x$）に対応付ければ離散圏とみなせます。

例2.2：行列と積

$1$以上の整数をいくつか集めた集合（たとえば$\cN \coloneqq \{1,2,4,8\}$）を対象の集まりとして，各$m,n \in \cN$に対して$m$行$n$列の行列（各成分は実数）を対象$n$から対象$m$への射とする圏（$\mathbf{Mat}$とおきます）が考えられます。2本の射$A$と$B$の合成は，行列としての積$BA$とします。$n$次単位行列が$n$上の恒等射です。

射の合成の例を示します。

圏!FORMULA[206][-958137872][0]における射の合成の例（!FORMULA[207][997696373][0]行列!FORMULA[208][36678][0]と!FORMULA[209][-799254955][0]行列!FORMULA[210][36647][0]の積は!FORMULA[211][997696373][0]行列!FORMULA[212][1137953][0]）圏$\mathbf{Mat}$における射の合成の例（$l \times m$行列$B$と$m \times n$行列$A$の積は$l \times m$行列$BA$）

補足：

この例において$\cN = \{n\}$（$n$は任意の自然数）の場合を考えると，例1.3で述べたモノイドになります。この意味で，例2.2は例1.3の一般化といえます。

例2.3：集合と写像

いくつかの集合の集まり$\cX \coloneqq \{X_1,X_2,\dots,X_n\}$を対象の集まりとして，各対象$X_i,X_j$に対して$X_i$から$X_j$への写像を対象$X_i$から対象$X_j$への射とする圏が考えられます。射の合成は写像の合成とします。$X_i$上の恒等写像（つまり$X_i$の各要素をその要素自身に写す写像）が$X_i$上の恒等射です。

さらに具体的な例として，（素朴な）プログラムの圏とでもいえるような圏$\mathbf{Prog}$を考えます。この圏における射の合成の例を示します。

圏!FORMULA[225][463917048][0]における射の合成の例圏$\mathbf{Prog}$における射の合成の例

ここで，$\mathrm{Int}$（整数全体），$\mathrm{Bool} \coloneqq \{\mathrm{true},\mathrm{false}\}$，$\mathrm{String}$（文字列全体）は$\mathbf{Prog}$の対象とします。この圏の射は関数で，対象は関数の引数や戻り値の型だと解釈できます（ここでは，「プログラム」らしさを出すために，写像のことを「関数」とよんでいます）。射$f \colon \mathrm{Int} \to \mathrm{Bool}$の例としては，奇数を$\mathrm{true}$に写して偶数を$\mathrm{false}$に写すような写像が考えられます。また，射$g \colon \mathrm{Bool} \to \mathrm{String}$の例としては，$\mathrm{true}$を文字列"odd"に写して$\mathrm{false}$を文字列"even"に写すような写像が考えられます。このとき射$gf \colon \mathrm{Int} \to \mathrm{String}$は，奇数を"odd"に写して偶数を"even"に写すような写像です。

補足：

例2.3を少し改良して，対象$X_i$から対象$X_j$への射をある特別な性質を満たす写像（たとえば線形写像や連続写像とよばれるようなもの）のみに限定することもできます。このような限定を考えたとき，例1.1や例2.2はこの特別な場合とみなせます。実際，例1.1は，例2.3において$\cX \coloneqq \{ \Natural \}$とおいて，写像を$\Natural \ni n \mapsto n + f \in \Natural$（ただし$f \in \Natural$）の形で表せるもののみに限定すれば得られます。また，例2.2において$k$個の要素から成る集合$\cN \coloneqq \{ n_1,n_2,\dots,n_k \}$を考えたとき，例2.3において$\cX \coloneqq \{\R^{n_1},\R^{n_2},\dots,\R^{n_k}\}$（ただし$\R^n$は$n$次元実列ベクトル全体）とおいて，写像を線形写像に限定すれば得られます。

例2.4：集合の圏$\Set$

例2.3の特別な場合として，すべての集合の集まりを対象の集まりとして，集合$X$から集合$Y$への写像を対象$X$から対象$Y$への射とする圏が考えられます。この圏を集合の圏とよび$\Set$と書きます。射$f$と射$g$の合成は写像としての合成$g \c f$であり，恒等射は恒等写像です。

この圏$\Set$を利用して任意の集合の要素を図式で表す方法を導入しておきます。この連載では，1個の要素から成る集合（1点集合とよびます）の一つを代表して$\{*\}$と書くことにします。任意の集合$X$とその要素$x \in X$を考え，$x$に対応する次の写像を考えます。
$$ \tilde{x} \colon \{*\} \ni * \mapsto x \in X $$
つまり，$\tilde{x}$は1点集合$\{*\}$の唯一の要素$*$を$X$の要素$x$に写すような写像です。この写像$\tilde{x}$は，明らかに$x$のみから一意に定まります。また，逆に$\tilde{x}$が与えられれば，$x$は$x = \tilde{x}(*)$と求まります。このため，$x$と$\tilde{x}$は本質的には同じものを表しているといえて，これらを同一視できます。以降ではこれらを同一視します。このとき，$x$（つまり$\tilde{x}$）は1点集合$\{*\}$から集合$X$への写像（つまり$\Set$の射）として，次の図式で表せます。

!FORMULA[279][-890499689][0]を写像!FORMULA[280][-1584452296][0]として表す $x \in X$を写像$* \mapsto x$として表す

この図式のように，1点集合$\{*\}$をグレーの点線で表し，ラベル「$\{*\}$」はしばしば省略します。

補足：

$X$の要素$x$と写像$\tilde{x}$を同一視するのは単に話を簡単にするためです。これらを同一視しなくても本質的に同じ議論が行えます。

例2.5：ベクトル空間の圏$\VecK$

任意の体$\K$について，$\K$上のすべてのベクトル空間の集まりを対象の集まりとして，ベクトル空間$\V$からベクトル空間$\W$への線形写像を対象$\V$から対象$\W$への射とする圏が考えられます。この圏をベクトル空間の圏とよび，$\VecK$と書きます。射$f$と射$g$の合成は写像としての合成$g \c f$であり，恒等射は恒等写像です。

また，圏$\VecK$と同様ですが，対象を有限次元ベクトル空間に限定した圏を有限次元ベクトル空間の圏とよび，$\FinVecK$と書きます。つまり，圏$\FinVecK$の対象は$\K$上の有限次元ベクトル空間で，射は線形写像で，射の合成は写像としての合成で，恒等射は恒等写像です。

補足：

体$\K$に不慣れな方は，$\K$を実数全体$\R$に読み替えても問題ありません。この場合，体$\K$上のベクトル空間とは$\R^n$のような実ベクトル空間のことです。また，線形写像に不慣れな方は，有限次元ベクトル空間のみを考えて，$n$次元ベクトル空間$\V$から$m$次元ベクトル空間$\W$への線形写像とは$m$行$n$列の実行列のことだと考えても概ね問題ありません。

例2.6：モノイドの圏$\Mon$

すべてのモノイドの集まりを対象の集まりとして，モノイド$\cM$からモノイド$\cN$へのモノイド準同型とよばれる写像を対象$\cM$から対象$\cN$への射とする圏が考えられます。この圏をモノイドの圏とよび$\Mon$と書きます。射$f$と射$g$の合成は写像としての合成$g \c f$であり，恒等射は恒等写像です。

補足：

モノイド準同型とは，直観的にはモノイドとしての性質を保つような写像のことです。具体的には，写像$f \colon \cM \to \cN$がモノイド準同型であるとは，(1)$f(b \c a) = f(b) \c f(a)$ $(\forall a,b \in \cM)$および(2)$f(1) = 1$を満たすことをいいます。なお，条件(1)は，各$a,b \in \cM$に対して「積をとってから$f$で写したもの」$f(b \c a)$が「それぞれを$f$で写してから積をとったもの」$f(b) \c f(a)$に等しいことを意味しています。このため，直観的には，「積をとる」ことと「$f$で写す」ことの順序を入れ替えられることといえます。条件(2)は，$f$が$\cM$の単位元$1$を$\cN$の単位元$1$に写すことを意味しています。なお，二つのモノイド準同型を合成したものがモノイド準同型になることや，恒等写像がモノイド準同型であることは，容易に確かめられます。

モノイド$\cM$がその任意の射$f,g$に対して$fg = gf$を満たすとき，可換であるとよびます。このとき，圏$\Mon$と同様ですが，対象を可換モノイドに限定した圏を可換モノイドの圏とよび$\CMon$と書きます。

例2.7：自然数と大小関係

自然数を対象とするような圏（$\mathbf{Pos}$とおきます）を考えます。ただし，各対象$x,y \in \Natural$について，この圏$\mathbf{Pos}$の$x$から$y$への射は$x \le y$ならば1本のみ存在して，$x > y$ならば存在しないものとします。これにより，$x$から$y$への射が存在することは$x \le y$であることと同値です。各$a \in \Natural$に対して$a \le a$ですので恒等射$1_a$が存在します。

射の合成の例を示します。$a \le b \le c$を満たす任意の$a,b,c \in \Natural$に対して，次式が成り立ちます。

圏!FORMULA[356][-954951196][0]における射の合成の例圏$\mathbf{Pos}$における射の合成の例

この式は，圏$\mathbf{Pos}$における射の合成を表しています。または，不等号$\le$が推移律（つまり$a \le b$かつ$b \le c$ならば$a \le c$であるという規則）を満たすことを表していると解釈できます。

まとめ

圏論における基本的な概念である圏の定義を示し，対象や射を図式（ストリング図）で表す方法を紹介しました。圏はある規則を満たすような対象の集まりと射の集まりのことといえます。図式を用いると，圏が満たすべき規則を視覚的に理解できると思います。今後の連載では，このような図式を積極的に用いて，圏論の基礎的な概念をわかりやすく説明したいと思います。