【ストリング図で学ぶ圏論 #3】垂直合成と水平合成

はじめに

今回の記事では，関手や自然変換の合成として，垂直合成と水平合成の2種類を説明します。また，これまでに登場したすべての合成がこれらの特別な場合とみなせることを述べます。図式では，これらの合成を，単に線やブロックをつなげることで表せます。

本連載の目次

#1： 圏の定義と具体例
#2： 関手と自然変換
#3： 垂直合成と水平合成（この記事）
#4： モノイダル圏
#5： モナドとは自己関手の圏におけるモノイド対象のこと
#6： モナドの例
#7： 随伴

垂直合成

まず，射としての合成である，垂直合成について説明します。

自然変換の垂直合成

2個の自然変換$\alpha \colon F \nto G$と$\beta \colon G \nto H$を任意に選びます（$F,G,H \colon \cC \to \cD$も任意です）。これらの各成分$\alpha_a \in \cD(Fa,Ga)$と$\beta_a \in \cD(Ga,Ha)$は$\cD$の射として合成できますので，合成により得られる（添字付けられた）射の集まり

$$ \beta\alpha \coloneqq \{ (\beta\alpha)_a \coloneqq \beta_a \alpha_a \}_{a \in \cC} $$

が考えられます。この集まりを，次の図式で表すことにします。

垂直合成$\beta\alpha$

この左辺が$\beta\alpha$を表しており，右辺の$\{~\}$内の式が$(\beta\alpha)_a \coloneqq \beta_a \alpha_a$を表しています。なお，破線を用いて$(\beta\alpha)_a$と$\beta_a \alpha_a$を表す図式を区別していますが，この定義によりこれらは等しいため，破線は単なる補助線と考えて削除しても問題ありません。

$\beta\alpha$は自然変換であること，つまり自然性

$$ Hf \c (\beta\alpha)_a = (\beta\alpha)_b \c Ff \qquad (\forall f \in \cC(a,b)) $$

を満たすことは，次式からわかります。

$\beta\alpha$の自然性の証明

ただし，左側および右側の等号ではそれぞれ$\beta$および$\alpha$の自然性を用いています。直観的には，この証明では単に3個のブロック$f$と$\beta$と$\alpha$を線に沿って動かしているだけだと解釈できます。自然変換$\beta\alpha$を，$\alpha$と$\beta$の垂直合成のようによびます。このように，図式では垂直合成を「縦方向の接続」により表します。

水平合成

次に，写像としての合成である水平合成について説明します。

関手同士の水平合成

まず，任意の$F \colon \cC \to \cD, ~G \colon \cD \to \cE$に対して，次の写像が考えられます。

$$ \mor \cC \ni f \quad\xmapsto{F}\quad F f \quad\xmapsto{G}\quad G(Ff) \in \mor \cE $$

この$\xmapsto{F}$および$\xmapsto{G}$は，それぞれ$F$および$G$の射への作用です。この写像を射への作用とするような$\cC$から$\cE$への関手が考えられ，この関手を$G \b F$と書きます（$G \b F$が関手であることはすぐに示せます）。また，この合成は$G$と$F$の水平合成（または合成）とよばれます。$G \b F$を次の図式で表すことにします。

$G \b F$

直観的には，線$G \b F$は右辺のように並列に並んだ2本の線$G$と$F$を横方向に移動させて重ねたものだと解釈できます。このように，図式では水平合成を「横方向に並べること」で表します。

自然変換同士の水平合成

2個の自然変換$\alpha \colon F \nto F'$（ただし$F,F' \colon \cC \to \cD$）と$\beta \colon G \nto G'$（ただし$G,G' \colon \cD \to \cE$）を任意に選びます。このとき，各対象$a \in \cC$に対して$\alpha_a$は$\cD$の射ですので，これを$\beta$の射への作用で写した射$\beta \b \alpha_a$が考えられます。 前回の記事 で述べた自然変換の射への作用の定義より，この射$\beta \b \alpha_a$は次のように表されます。

射$\beta \b \alpha_a$

直観的には，この図式は単にブロック$\beta$と$\alpha$を線に沿って動かしているだけといえます。ここで，次の射の集まり

$$ \beta \b \alpha \coloneqq \{ \beta \b \alpha_a \}_{a \in \cC} $$

を考えます。これは，次の写像を考えていることと本質的に同じです。

$$ \ob \cC \ni a \quad\xmapsto{\alpha}\quad \alpha_a \quad\xmapsto{\beta}\quad \beta \b \alpha_a \in \mor \cE $$

ただし，$\xmapsto{\alpha}$は$\alpha$の対象への作用を表しており，$\xmapsto{\beta}$は$\beta$の射への作用を表しています。このとき，$\beta \b \alpha$は$G \b F$から$G' \b F'$への自然変換です。このことを示すためには，自然性を満たす，つまり

$$ (G' \b F')f \c (\beta\alpha)_a = (\beta\alpha)_b \c (G \b F)f \qquad (\forall f \in \cC(a,b)) $$

を満たすことを示せば十分ですが，これは次式からわかります。

$\beta \b \alpha$の自然性 $$\tag{1}\label{eq:beta_alpha_f}$$

ただし，2番目および3番目の等号では，それぞれ$\alpha$および$\beta$の自然性を用いました。念のためていねいに式変形していますが，直観的には3個のブロック$f$と$\beta$と$\alpha$を単に線に沿って動かしているだけだと解釈できます。

$\beta \b \alpha$を，次の左側または右側の図式で表すことにします。

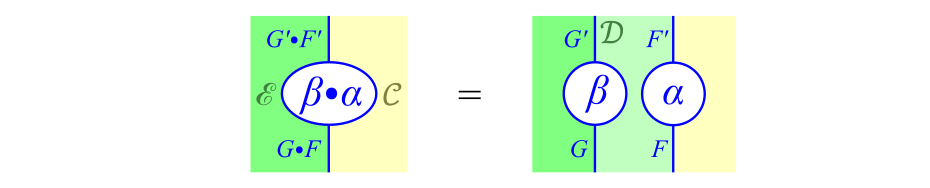画像の名前

この$\beta \b \alpha$を$\beta$と$\alpha$の水平合成とよびます。なお，$\beta \b \alpha$の射への作用は，次の写像です。

$$ \mor \cC \ni f \quad\xmapsto{\alpha}\quad \alpha \b f \quad\xmapsto{\beta}\quad \beta \b (\alpha \b f) \in \mor \cE $$

この$\xmapsto{\alpha}$および$\xmapsto{\beta}$はそれぞれ$\alpha$および$\beta$の射への作用です。$\beta \b (\alpha \b f)$は式\eqref{eq:beta_alpha_f}の1番左側の式で表されます。

関手と自然変換の水平合成

恒等自然変換$1_G$と自然変換$\alpha$の水平合成$1_G \b \alpha$を$G \b \alpha$と書きます。これを，関手$G$と自然変換$\alpha$の水平合成とみなします（直観的には，恒等自然変換$1_G$は関手$G$のようなものといえます）。

同様に，自然変換$\beta$と恒等自然変換$1_F$の水平合成$\beta \b 1_F$を$\beta \b F$と書きます。これを，自然変換$\beta$と関手$F$の水平合成とみなします。

これらは，次のような図式で表されます。

$G \b \alpha$と$\beta \b F$

垂直合成と水平合成

これまでに登場した合成はすべて垂直合成・水平合成とみなせる

前回の記事 で触れたように，任意の対象は関手とみなせて，任意の射は自然変換とみなせるのでした。このようにみなせば，これまでに述べてきた合成は，すべて今回の記事で述べた垂直合成または水平合成として捉えられます。「図式において線で表されているもの（つまり対象と関手）はすべて関手とみなせて，ブロックで表されているもの（つまり射と自然変換）はすべて自然変換とみなせる」と考えるとわかりやすいと思います。

具体的に述べます。まず，圏$\cC$の2本の射$f \colon a \to b$と$g \colon b \to c$は，次のように合成できるのでした。

射の合成$gf$

一方，これらの射$f,g$は自然変換とみなせます。このようにみなすと，この合成は自然変換$f,g$の垂直合成にほかなりません。

次に，関手$F \colon \cC \to \cD$について考えます。$F$は$\cC$の対象$a$と射$f$をそれぞれ$\cD$の対象$Fa$と射$Ff$に写し，これらを次の図式で表すのでした。

$Fa$と$Ff$

一方，対象$a$は関手とみなせて射$f$は自然変換とみなせます。このとき，$Fa$は2個の関手$F,a$の水平合成$F \b a$とみなせます。また，$Ff$は関手$F$と自然変換$f$の水平合成とみなせます。

自然変換$\alpha \colon F \nto G$（ただし$F,G \colon \cC \to \cD$）についても同様です。$\alpha$は$\cC$の対象$a$と射$f$をそれぞれ$\cD$の射$\alpha_a$と射$\alpha \b f$に写し，これらを次の図式で表すのでした。

$\alpha_a$と$\alpha \b f$

対象$a$を関手とみなして射$f$を自然変換とみなすと，$\alpha_a$は自然変換$\alpha$と関手$a$の水平合成$\alpha \b a$とみなせて，$\alpha \b f$は自然変換$\alpha,f$の水平合成とみなせます。

このように，これまでに登場した合成はすべて垂直合成または水平合成として統一的に扱えます。

垂直合成と水平合成が混在したときの規則

垂直合成と水平合成が混在すると何が起こるでしょうか？たとえば

$(\beta' \c \beta) \b (\alpha' \c \alpha) = (\beta' \b \alpha') \c (\beta \b \alpha)$ $$\tag{1}\label{eq:1}$$

のように，「垂直合成してから水平合成した結果」と「水平合成してから垂直合成した結果」は等しくなるでしょうか？（なお，図式から$F,F',F'' \colon \cC \to \cD$や$\alpha \colon F \nto F'$などがわかります）。より複雑な合成ではどうなるでしょうか？

実は，複数の自然変換を垂直合成と水平合成により合成して得られる自然変換は，その合成の順序によらないことを示せます（証明は割愛します）。このため，たとえば上記の式の補助線を消してもこれらは等しいため問題ありません。それぞれの自然変換は線に沿って縦方向に自由に移動できますので，たとえば次式が成り立ちます。

自然変換$\alpha,\beta,\gamma,\delta$の合成により得られる自然変換 $$\tag{2}\label{eq:abcd}$$

ただし，この式に現れる自然変換$\alpha,\beta,\gamma,\delta$（と関手）は任意です。なお，この左辺では4個の自然変換$\alpha,\beta,\gamma,\delta$と3個の関手$F'',G',H$との垂直合成や水平合成により構成されていることがわかるように，補助線（破線）を描いています。数式で表すと

$$ (\alpha \b F'') \c (\beta \b G' \b \gamma) \c (H \b \delta) = (\alpha \b \gamma) \c (\beta \b \delta) $$ $$\tag{3}\label{eq:abcd_formula}$$

です。この式のように複雑な図式が現れたら，適切に破線を引くことで小さな単位に分解して考えれば，自然変換がどのように合成されているかがわかります。

図式で表すことのメリット

図式\eqref{eq:abcd}と数式\eqref{eq:abcd_formula}とを比べてみてください。多くの人にとって，図式のほうがわかりやすいと感じるのではないでしょうか？今回の例では，主な理由として以下の二つが挙げられそうです。

1. 多くの情報を素直に埋め込める：たとえば図式では，$\beta$が$H$から$H'$への自然変換であることがわかります。なお，数式でこれらの情報を付与することもできますが，煩雑になります。
2. 2次元的に表せる：数式では横一列で（1次元的に）表すことになるため，「縦方向と横方向にどのようにつながっているか」を即座には理解しにくいと思います。これに対し，図式では2次元的に表せるため，この問題が解消されます。このため，数式\eqref{eq:abcd_formula}では等号がなぜ成り立つのかがわかりにくいのに対し，図式\eqref{eq:abcd}の等号が成り立つことは自明に思えると思います。

このように，少し複雑な式においては，数式よりも図式のほうがわかりやすいことが少なからずあります。

関手圏$\cD^\cC$

最後に，関手圏についても紹介しておきます。これまでに述べたように，任意の対象は関手とみなせて任意の射は自然変換とみなせます。実は，この逆も成り立ちます。具体的には，これから説明する関手圏を考えれば，任意の関手は対象とみなせて任意の自然変換は射とみなせます。

任意の圏$\cC,\cD$に対して，次のような圏を関手圏とよび，$\cD^\cC$と書きます。

• 対象は，$\cC$から$\cD$への関手である。
• 対象（つまり関手）$F \colon \cC \to \cD$から対象（つまり関手）$G \colon \cC \to \cD$への射は，$F$から$G$への自然変換である。
• 射の合成は自然変換の垂直合成であり，恒等射は恒等自然変換である。

このように，関手圏では関手を対象として自然変換を射とします。自然変換の垂直合成の定義から，自然変換$\alpha \colon F \nto G$と恒等自然変換$1_F,1_G$について，$\alpha 1_F = \alpha = 1_G \alpha$，つまり

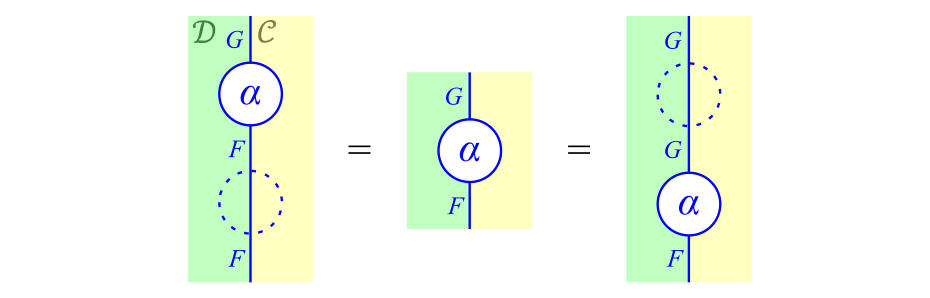単位律

が成り立つことがすぐにわかります。ただし，恒等自然変換を破線のブロックで表しています（この破線は単なる補助線とみなせて，省略しても問題ありません）。この式は，関手圏$\cD^\cC$における単位律にほかなりません。$\cD^\cC$が結合律も満たし，したがって$\cD^\cC$が圏であることが容易にわかります（証明は割愛します）。なお，$\cD^\cC$の射（つまり自然変換）が同型射であることは，自然同型であることと同値です（証明は割愛します）。

任意の圏$\cE$の対象$a$と恒等射$1_a$を同一視しても本質的には問題ないのでした（ 第1回の記事 を参照のこと）。このため，$\cD^\cC$の各対象（つまり関手）$F$は$\cD^\cC$の恒等射（つまり恒等自然変換）$1_F$と同一視しても，本質的には問題ありません。

まとめ

自然変換を合成する2種類の方法（垂直合成と水平合成）を説明しました。垂直合成は射の合成に相当し，水平合成は写像としての合成に相当するのでした。図式では垂直合成および水平合成を，それぞれ「縦方向」および「横方向」の合成として表せます。図式により，これらの合成を視覚的に表せて，かつ少し慣れればこれらを即座に区別できるようになると思います。