【ストリング図で学ぶ圏論 #4】モノイダル圏

はじめに

この記事では，圏の特別な場合である，モノイダル圏について紹介します。

圏は射の合成という演算を備えており，ストリング図ではこれを「直列接続」として表せるのでした。モノイダル圏は，モノイド積という演算を備えた圏として定められます。また，ストリング図では，これを「並列接続」として表せます。直観的には，モノイダル圏とは「ブロックの直列接続と並列接続が行えて，これらの接続が素直な性質を満たすもの」であるといえます。

本連載の目次

#1： 圏の定義と具体例
#2： 関手と自然変換
#3： 垂直合成と水平合成
#4： モノイダル圏（この記事）
#5： モナドとは自己関手の圏におけるモノイド対象のこと
#6： モナドの例
#7： 随伴

モノイダル圏

厳密モノイダル圏

まず，モノイダル圏よりも直観的に理解しやすいと思われる，厳密モノイダル圏について説明します。

厳密モノイダル圏の定義

厳密モノイダル圏は，次のように定義されます。

これらの規則は，図式を用いてわかりやすく表せます。図式では，任意の対象$a,b \in \cC$に対して対象$a \ot b \in \cC$を（2本の線$a,b$の「並列接続」として）次のように表すことにします。

$a \ot b$

同様に，任意の射$f,g \in \mor \cC$に対して射$f \ot g \in \mor \cC$を（2個のブロック$f,g$の「並列接続」として）次のように表すことにします。

$f \ot g$

なお，本文中では省略した射$f$のドメインとコドメインに関する情報を，図式では明記しています（ドメインが$a$でコドメインが$a'$です）。射$g$についても同様です。以降でも，図式に含まれている情報の一部を本文中では省略することがあります。

このとき，条件(1)の結合律は次式のように表せます。

結合律$(f \ot g) \ot h = f \ot (g \ot h)$

この規則は，直観的には「3個以上のブロックを並列接続したとき，その接続の結果は接続の順序に依存しない」と解釈できます。また，上の図式の両辺のドメインに着目すると，$\cC$の任意の対象$a,b,c$について$(a \ot b) \ot c = a \ot (b \ot c)$が成り立つことがわかります。

また，条件(2)の単位律は次式のように表せます。

単位律$1_i \ot f = f = f \ot 1_i$

ただし，単位対象$i$をグレーの線で表しています（恒等射は対象と実質的に同一視できて線として表せるのでした）。この規則は，直観的には「グレーの線を省略しても問題ない」と解釈できます。また，この規則から，$\cC$の任意の対象$a$について$i \ot a = a = a \ot i$が成り立つことがわかります。

ある演算が結合律と単位律を満たすとき，暫定的に「モノイド的」とよぶことにします。大まかに述べると，厳密モノイダル圏とは，射の合成（つまり縦方向の接続）とモノイド積（つまり横方向の接続）の両方に関して「モノイド的」であるような圏のことといえます。

厳密モノイダル圏の基本的な性質

モノイド積$\ot$は関手ですので，合成を保ちます。つまり，$\cC \times \cC$の任意の2本の射$\braket{f,g}$と$\braket{f',g'}$ について，これらが合成可能ならば$f'f \ot g'g = (f' \ot g')(f \ot g)$を満たします。この式は，次の図式で表せます。

$f'f \ot g'g = (f' \ot g')(f \ot g)$
$$\tag{1}\label{eq:1}$$

この式は，直観的には「直列接続と並列接続が混在していたときに，その接続の結果は接続の順序に依存しない」と解釈できます。なお，この図式では縦方向と横方向にそれぞれ2個ずつのブロックが並んでいますが，3個以上のブロックが並んだ場合にも同様に接続の順序に依存しないことを示せます。

また，モノイド積$\ot$は関手ですので，各恒等射を恒等射に写します。つまり，任意の$a,b \in \cC$について$1_a \ot 1_b = 1_{a \ot b}$を満たします。この式は次の図式で表せます。

$1_a \ot 1_b = 1_{a \ot b}$

この式は，直観的には「線$1_{a \ot b}$は2本の線$1_a$と$1_b$ を束ねたもの」と解釈できます。

射の合成における単位律と式\eqref{eq:1}より，次式（スライディング則などとよばれます）が成り立つことがわかります。

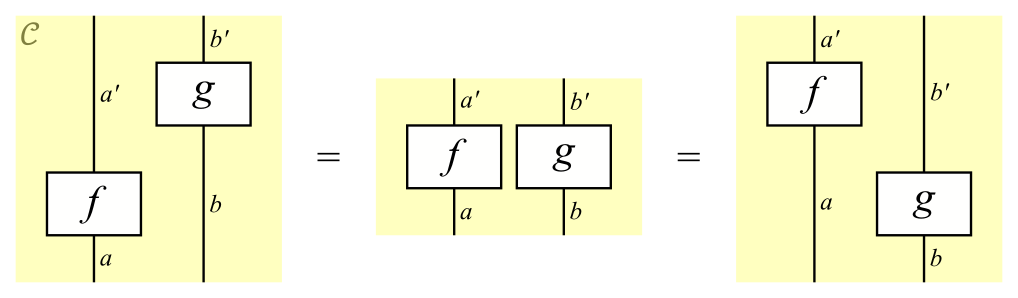スライディング則

この式は，直観的には「射$f$や射$g$を線に沿って上下方向に動かしても値は変わらない」と解釈できます。

このように，モノイダル圏ではブロックの直列接続（合成）と並列接続（モノイド積）という演算が行えます。これらの接続が満たすべき性質は，いずれも素直そうだと感じるのではないかと思います。

モノイダル圏

モノイダル圏は，厳密モノイダル圏を一般化した概念です。厳密な定義は拙著Nak-2024に委ね，ここでは大まかな説明のみをします。厳密モノイダル圏では対象$a,b,c \in \cC$に関する結合律$a \ot (b \ot c) = (a \ot b) \ot c$が成り立つのでした。これに対し，モノイダル圏では，この等号を同型に置き換えた$a \ot (b \ot c) \cong (a \ot b) \ot c$を考えます。また，対象$a$に関する単位律$i \ot a = a = a \ot i$の等号を同型に置き換えた$i \ot a \cong a \cong a \ot i$を考えます。モノイダル圏は，これらの同型が自然であり，かつある意味において素直な条件（コヒーレント条件とよばれます）を満たすものとして定められます。

モノイダル圏の定義はやや複雑です。しかし，任意のモノイダル圏は，厳密モノイダル圏と同じ図式を用いて表せることが知られています。このため，厳密モノイダル圏と同様に，図式を用いて視覚的にわかりやすく表せます。

モノイダル圏の例

モノイダル圏の例は数多くありますが，ここではその一部のみを紹介します。

自己関手の圏$\cC^\cC$

任意の圏$\cC$について，関手圏$\cC^\cC$（自己関手の圏とよばれます）と水平合成$\b$と恒等関手$1_\cC$の組$\braket{\cC^\cC,\b,1_\cC}$はモノイダル圏（とくに厳密モノイダル圏）です。関手圏は， 第3回の記事 で紹介しました。なお，関手$F \colon \cC \to \cC$は，しばしば$\cC$上の自己関手とよばれます。

自然変換$\beta \in \mor \cC^\cC$と自然変換$\alpha \in \mor \cC^\cC$のモノイド積は水平合成$\beta \b \alpha$です。

$\cC^\cC$におけるモノイド積（水平合成）$\beta \b \alpha$

集合の圏$\Set$

集合の圏$\Set$は，直積$\times$をモノイド積として1点集合$\{*\}$を単位対象とするモノイダル圏とみなせます。つまり，$\braket{\Set,\times,\{*\}}$はモノイダル圏です（厳密モノイダル圏ではありません）。写像$f \colon X \to X'$と写像$g \colon Y \to Y'$のモノイド積はデカルト積$f \times g$（つまり，写像$X \times Y \ni \braket{x,y} \mapsto \braket{f(x),g(y)} \in X' \times Y'$）です。

$\Set$におけるモノイド積（デカルト積）$f \times g$

ベクトル空間の圏$\VecK$

ベクトル空間の圏$\VecK$は，ベクトル空間の直和$\oplus$をモノイド積として0次元ベクトル空間$\{\zero\}$を単位対象とするモノイダル圏とみなせます。つまり，$\braket{\VecK,\oplus,\{\zero\}}$はモノイダル圏です（厳密モノイダル圏ではありません）。線形写像$f \colon \V \to \V'$と線形写像$g \colon \W \to \W'$のモノイド積は直和$f \oplus g$（つまり，線形写像$\V \oplus \W \ni v \oplus w \mapsto f(v) \oplus g(w) \in \V' \oplus \W'$）です。

$\braket{\VecK,\oplus,\{\zero\}}$におけるモノイド積（直和）$f \oplus g$

ベクトル空間の圏$\VecK$は，ベクトル空間のテンソル積$\ot$をモノイド積としてベクトル空間$\K$を単位対象とするモノイダル圏ともみなせます。つまり，$\braket{\VecK,\ot,\K}$もモノイダル圏です（厳密モノイダル圏ではありません）。

$\braket{\VecK,\ot,\K}$におけるモノイド積（テンソル積）$f \ot g$

なお，このモノイダル圏は上のモノイダル圏$\braket{\VecK,\oplus,\{\zero\}}$とは異なりますので，図式では念のため背景色を変えて表しています。

自然数と大小関係

第1回の記事 では，自然数（$0$以上の整数）を対象として大小関係を射とする圏$\mathbf{Pos}$を紹介しました。この圏$\mathbf{Pos}$は，自然数の和$+$をモノイド積として$0$を単位対象とする厳密モノイダル圏とみなせます。つまり，$\braket{\mathbf{Pos},+,0}$は厳密モノイダル圏です。

対象（つまり自然数）$a$から対象$a'$への射は，高々1本のみ存在して，この射が存在することは$a \le a'$を意味するのでした。この射を「$a \le a'$」と表すことにします。射「$a \le a'$」と射「$b \le b'$」のモノイド積は，射「$a + b \le a' + b'$」です。$a \le a'$と$b \le b'$が成り立つならば，$a + b \le a' + b'$が成り立ちますので，この射が存在します。

$\braket{\mathbf{Pos},+,0}$におけるモノイド積

プログラム

第1回の記事 では，プログラムの圏$\mathbf{Prob}$を紹介しました。この圏は，「並列接続」をモノイド積とするモノイダル圏とみなせます。たとえば，次の図式

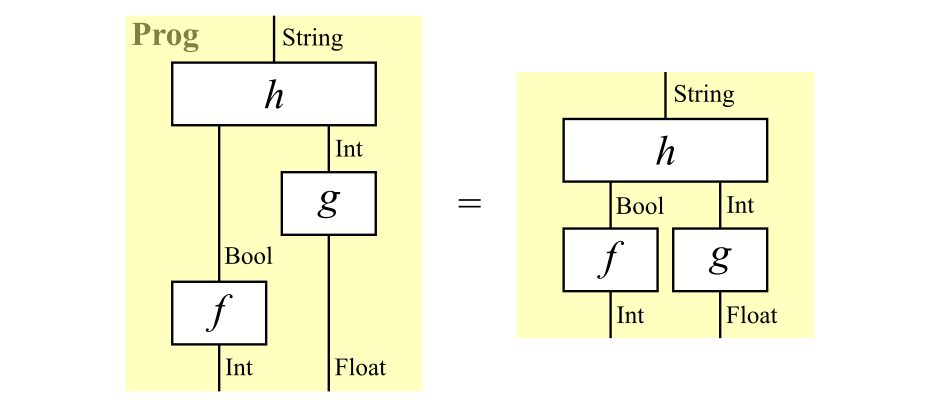プログラム

の左辺は，「関数$f$と関数$g$を順に施してから，それらの関数の両方の出力に対して関数$h$を施す」という処理を表します。この式の等号が成り立ちますので，関数$f$と関数$g$を同時に施しても結果は変わりません。なお，単位対象は1個の値のみをもつ自明な型です。

まとめ

直列接続に加えて並列接続を備えた圏である，モノイダル圏を紹介しました。最後の例で紹介したプログラムの圏と同様に，さまざまな作業手順（たとえば料理のレシピ）もモノイダル圏とみなせます。このような観点で眺めれば，モノイダル圏は日常生活のいろいろな場面で現れることに気が付くと思います。