今まで書いてきた記事の紹介とGoogle検索

はじめに

　この記事では私が今まで書いてきた百何十本の記事がGoogle検索でどの程度ヒットするのかをニコニコしながら検証していきます。ついでに私の書いてきた記事を簡単に紹介していきます。

Mathlogを今後より良いサービスにしていくために、しばらくはどんどん新機能を追加していくのではなく、

・データのバックアップ
・サーバーの安定化
・現状の機能の向上
・Googleの検索順位の向上

をより丁寧に行っていこうと思います。

— Mathlog 公式 【3500記事突破】 (@MathlogOfficial) January 4, 2021

　Mathlogがリリースされた初期のころに公式がこのようにアナウンスしていたように、Mathlogの記事はGoogleの検索結果において比較的上の方に出てくるように取り計らわれているらしいです。例えば「ラマヌジャン　円周率」と検索すると上から三番目に 私の記事 が躍り出てきます( 便利さんの記事 の方が上に出て来るのが少し悔しい)。
検索例

　特に私の書く記事は日本語文献の少ないニッチな話題に関するものが多いので特に検索上位に躍り出やすいものと推測されます。では実際今まで書いてきた記事についてGoogleで検索してみるとどのくらいヒットするのでしょうか。私のエゴサ以上の需要があるかはわかりませんが、それとなく検証していきましょう。
　なお私の記事の一覧については こちらの記事 にまとめてありますので、この記事を読んで興味を持ったものがあればそちらからチェックしてみてください。

検証

正則素数編

　こちらはフェルマーの最終定理やベルヌーイ数と正則素数との関係についての証明をまとめたシリーズとなります。最初期に書いた記事なので記事の書き方にかなりクセがあります。
　「正則素数」だけだとFLTの記事が9番目くらいに出るだけでしたが、「フェルマーの最終定理」や「ベルヌーイ数」とセットだとかなり上位に出ました。他に補題として書いた記事も「円分体」「クンマーの補題」「類数公式」といった検索ワードで上位の方に出るようです。
検索結果

$k$-ナッチ数編

　こちらは当時 apu_yokai さんが熱を入れていた$k$-ナッチ数(フィボナッチ数の一般化の一種)について個人的に考察したシリーズとなります。
　「$k$ナッチ数」だけだとapu_yokaiさんの記事が上に挙がりますが、「四捨五入」まで入れると私の記事が一番上に来ました。補題に書いた記事も「ヴァンデルモンド　逆行列」で出てきますね。
検索結果

複素解析・$p$進解析編

　こちらはゼータ関数、モジュラー形式関連の記事の基盤となる基礎知識についてまとめたものとなります。$p$進解析についてはかなり興味本位で書いています。
　特筆すべきことは特にないですね。
検索結果

円周率公式編

　こちらはラマヌジャンの円周率公式
$$\frac1\pi=\frac{2\sqrt2}{99^2}\sum^\infty_{n=0}\frac{(4n)!}{(n!)^4}\frac{26390n+1103}{396^{4n}}$$
やChudnovskyの円周率公式
$$\farc1\pi=12\sum_{n=0}^\infty(-1)^k\frac{(6n)!}{(3n)!(n!)^3}\frac{545140134n+13591409}{640320^{3n+\frac32}}$$
について理解しようと奔走したシリーズとなります。
　この記事群で扱ったトピックは多いですがそのどれもが上位に出てくるっぽいですね(超幾何関数、モジュラー形式、楕円関数、モジュラー方程式、二平方定理の一般化、etc...)。
検索結果

リーマン予想編

　こちらはリーマン予想に関係する色々な命題についてまとめたシリーズとなります。これも最初期に書いたものなので記事の書き方に少しクセがあります。
　リーマン予想についてはやはり色々なメディアが取り上げているため、私の記事の中でも 一番高評価の多い記事 ですら検索順位は低いですね。ただやはり素数公式やラマヌジャンの定理といった込み入った話となると上位に出てくるようです。
検索結果

代数的整数論編

　こちらは$p$進数による整数論へのアプローチについて紹介するシリーズとなります。
　ちなみにこのシリーズはクロネッカー・ウェーバーの定理の証明を最終目標として書き始めており、実際証明の流れまでは理解し終えていたのですが、それを記事にするとなると書かなければいけないことが多すぎるということで筆を投げてしまったシリーズとなっています。今もなお記事の下書き一覧には何かを書こうとした跡が残っています。
記事の残骸
　特筆すべきことは特にありません。
検索結果

雑学

　こちらは雑学的な内容の記事群となります。いくつかピックアップして紹介していきましょう。

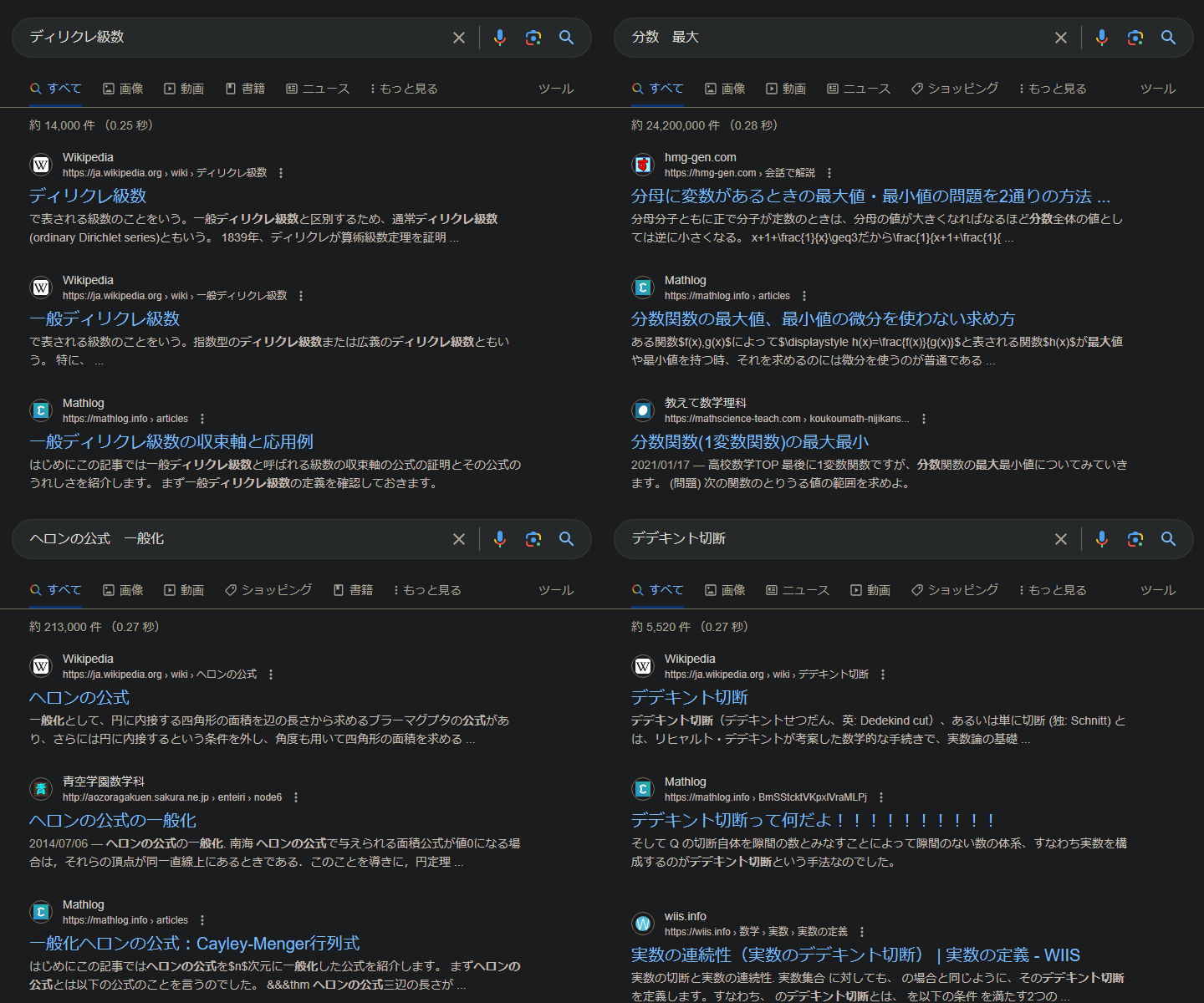
• 一般ディリクレ級数の収束軸と応用例
  ディリクレ級数$\sum^\infty_{n=1}a_ne^{-\la_n s}$がどのような$s$に対して収束するのか明示的に求める公式、およびその使い方について解説しています。
• 分数関数の最大値、最小値の微分を使わない求め方
  私が高校の頃に思い付いた分数関数の最大・最小問題に対する手法について解説しています。なぜか閲覧数も高評価数も多くて驚いています。
• 一般化ヘロンの公式：Cayley-Menger行列式
  三辺の長さから三角形の面積を求める公式：ヘロンの公式の$n$次元図形(錐体)への一般化について解説しています。先日 AKITO さんがした ツイート からこの記事に辿り着いている人がちらほらいましたね。
• スターリングの公式の簡単な証明
  スターリングの公式は一本の等式$\dis\sqrt{t}\l(\frac{e}{t}\r)^t\G(t)=\int^\infty_{-\infty}\exp\l(t(1+\frac{x}{\sqrt{t}}-e^{\frac{x}{\sqrt{t}}})\r)dx$だけで説明できます。
• リンデマン・ワイエルシュトラスの定理
  超越数論における有名な定理の英語版Wikipediaを日本語に訳した記事です。
• 二項係数の素因数と合同関係と東大数学2021
  二項係数の合同関係についての一般論とそれを用いた東大数学の解法を紹介しています。検索には引っかかりにくいのが悲しいところ。
• デデキント切断って何だよ！！！！！！！！！！
  数学科の人が最初に躓きやすい概念の一つ、デデキント切断について個人的な見解を示しています。
• 整数が二次形式で表現できる条件と応用例
  整数$n$が$n=ax^2+bxy+cy^2$と表せるための条件とその表現の求め方について紹介しています。
  検索結果

自由研究

　こちらは私が個人的に考えて発見したことなどについてまとめた記事群となります。雑学と自由研究との分類が曖昧になっている節があります。

• coth xの部分分数展開とsinh xの因数分解公式の初等的証明
  私が高校の頃に考えた問題について解説しています。
• N進じゃない位取り記数法
  一般の位取り記数法についてその扱いやすさについて考察しています。
• 36進法は"いい"記数法説
  上の記事に類似して36進法の利便性について提案しています。
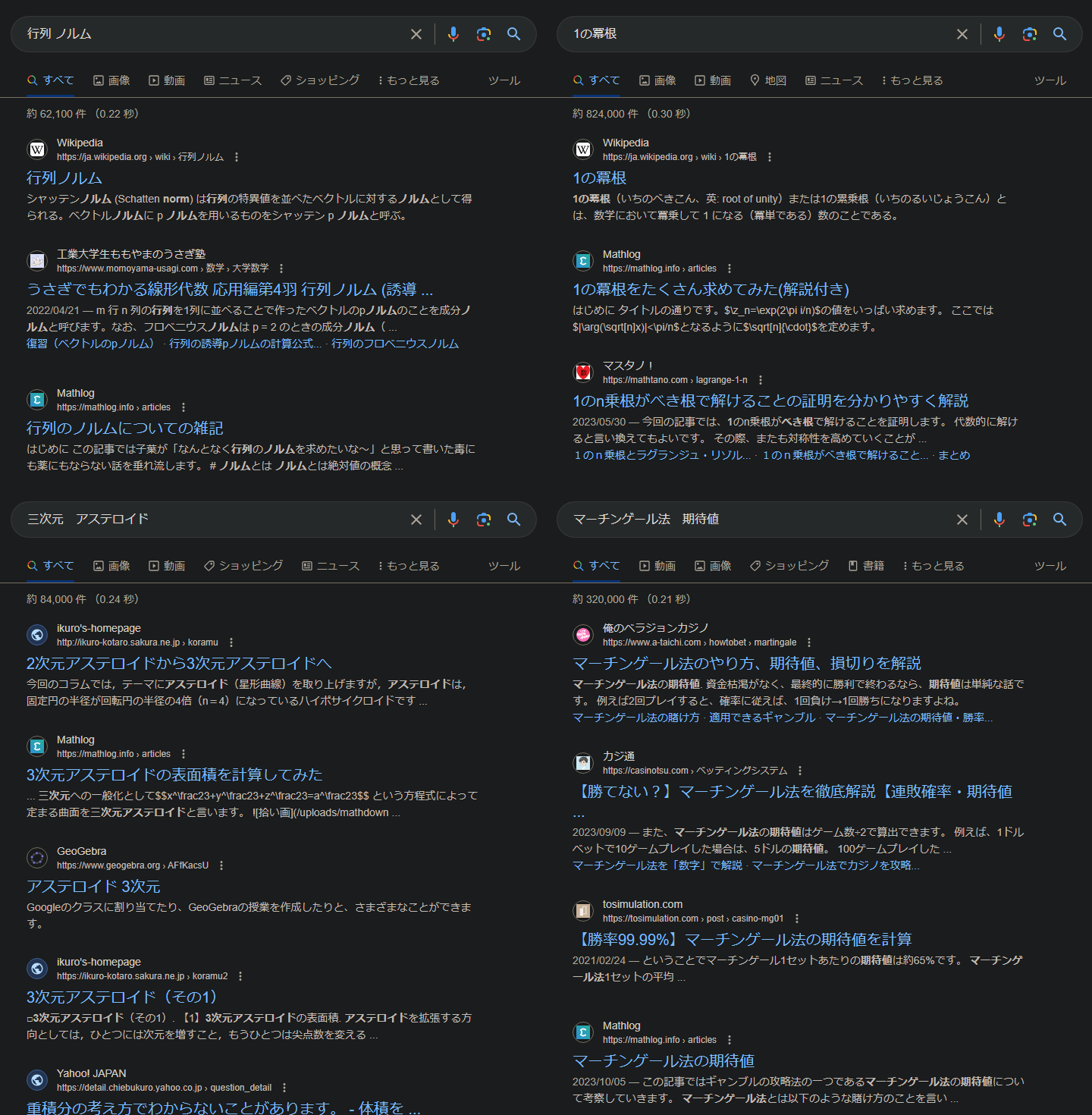
• 行列のノルムについての雑記
  函数解析の勉強をしていたとき、ふと行列のノルムはどのように求まるのか気になって色々調べた記事となります。
• 四次方程式の解の公式を解剖してみる
  一般に五次以上の方程式は(代数的に)解けないことが知られていますが、四次・三次の方程式についてはその構造を明らかにすることができます。
• 1の冪根をたくさん求めてみた(解説付き)
  五次方程式が解けないことの副産物として1の冪根は代数的に求められることが知られています。
• 3次元アステロイドの表面積を計算してみた
  暴力的な計算量を誇ると話題の問題を解いてみました。
• マーチンゲール法の期待値
  ギャンブルの必勝法の期待値を数学的に求めてみました。確率が丁度$1/2$なら絶対に勝てます(良い子はマネしないでね)。
  検索結果

おわりに

　上で紹介した検索例は一枚のスクショに収まる範囲に表示されたものだけを挙げており、全部が全部検索に引っかかったわけではありませんでしたが、それにしても引っかかりすぎなくらいです。
　こうして自分の書いた記事が人の目に留まる機会があるというのは嬉しいものですね。しかし裏を返せばどんなに粗悪な記事でも多くの人の目に晒される可能性があると考えると、もう少し責任感を持って記事を書いていかねばと思わされます。特に私が最初期に書いた記事たちは目に余るところが多いのでいつかちゃんと書き直したいですね。
　なにはともあれ皆様も多くの人に見てもらいたいお話があれば、この情報共有サイト：Mathlogに記事を書いてみてはいかがでしょうか。